二分查找

思想 #

二分查找的思想是，在有序序列中寻找目标值（目标的定义每题不同），通过比较中间元素，每次将空间缩小一半。是“分治法（Divide and Conquer）”最纯粹的例子之一

每次比较排除一半元素：

$$ T(n)=T(\frac{n}{2})+O(1)，解得 T(n) = O(\log_2{n}) $$

虽然思想很简单，但是实现时需要考虑很多细节，不然可能会产生错误

“Although the basic idea of binary search is comparatively straightforward, the details can be surprisingly tricky…” — Donald Knuth.

常见错误 #

以下代码展示了一个看起来“没问题”的 Pascal 版二分查找，但实际上包含多个错误。

这段 Pascal 代码摘自 Richard E. Pattis 于 1988 年发表的论文《Textbook Errors in Binary Searching》。 他查阅了二十本教材，发现它们中普遍使用了这样的二分查找实现。（在 Pascal 语言中，数组的下标从 1 开始。）

PROCEDURE BinarySearch (A         : anArray,
                        Size      : anArraySize,
                        Key       : INTEGER,
                        VAR Found : BOOLEAN;
                        VAR Index : anArrayIndex);
Var Low, High : anArrayIndex;
BEGIN         
   LOW := 1;
   High := Size;
   
   REPEAT
      Index := (Low + High) DIV 2;
      If Key < A[Index]
         THEN High := Index - 1
         ELSE Low  := Index + 1
   UNTIL (Low > High) OR (Key = A[Index]);

   FOUND := (Low <= High)
END;

错误 1 没有在 O(log n) 时间复杂度下运行 #

问题不在循环逻辑本身，而在函数参数传递方式。

代码中的 A : anArray 是按值传参的。在 Pascal（或 C++）中，如果你把整个数组以值传递给函数（不是以引用/指针），编译器会复制整个数组到函数的栈或临时内存。

数组复制操作的时间复杂度是 O(n)，二分查找本身的逻辑是 O(log n)，于是总体复杂度变成 O(n)，失去了“对数查找”的意义。有些程序员甚至写递归版二分查找，每次递归调用都再次复制整个数组，这种情况下时间复杂度更糟糕。

错误 2 size = 0 #

如果 Low = 1、High = 0，再去访问 A[(Low + High) DIV 2] 就会越界，所以须在实现中加上 if Size = 0 then exit; 或类似的边界检查

错误 3 size = 1 #

如果最后一次迭代开始时Low = High （例如数组大小为 1 时），则进入到ELSE分支 Low := Index + 1，Low = 2 > High = 1 退出循环，即使 Key 实际上存在于数组中，程序也会将 Found := (Low <= High) 设为 False，导致找不到目标值

错误 4 目标值小于最小元素 #

当 Index 取值为 1 时，代码会将 High 设为 0，从而导致数组下标越界等错误。（上面的代码 UNTIL (Low > High) OR (Key = A[Index]) 立刻为真（1 > 0），于是本轮结束后直接退出，不会出现此错误，但是其他版本可能会出现）

错误 5 目标值大于最大元素 #

当 Index 取值为 Size 时，代码会将 Low 设为 Size + 1，从而导致数组下标越界等错误。（上面的代码 UNTIL (Low > High) OR (Key = A[Index]) 立刻为真（Size+1 > Size），于是本轮结束后直接退出，不会出现此错误，但是其他版本可能会出现）

通用解法 #

题目要求的目标值可能每道题目都不同，通常我们会对模板二分查找代码修改，但是具体怎么修改可能毫无头绪或者错误百出。

这里介绍一种简单、通用的思路，将二分查找的low、high边界赋予特定的含义（红蓝边界），来解决大部分二分查找问题。

参看下面题目：

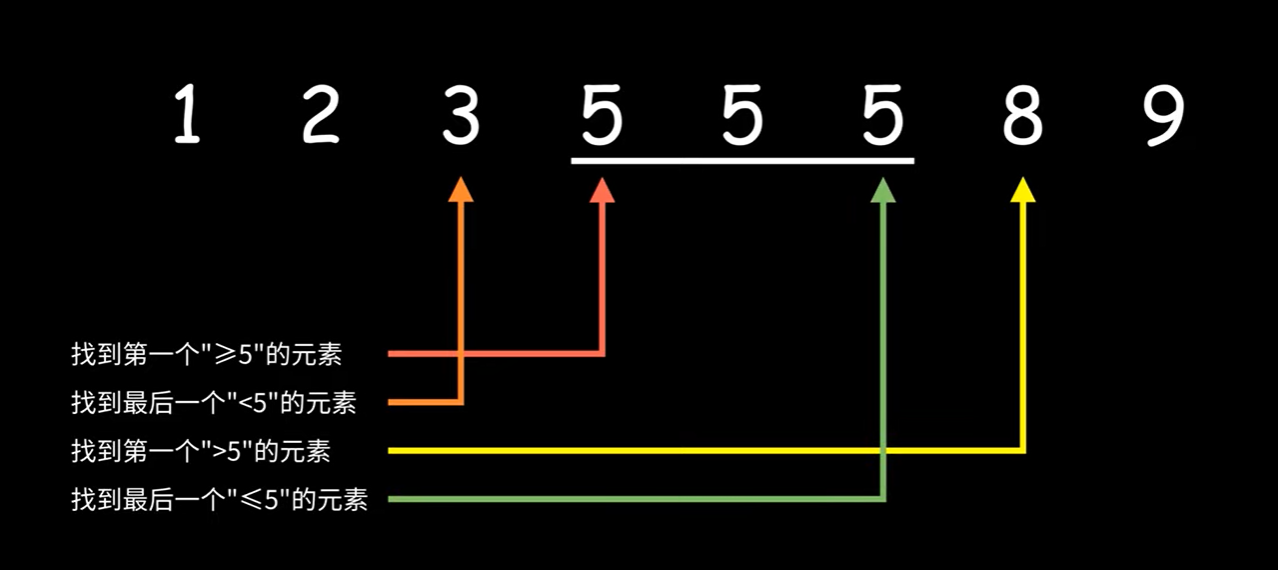
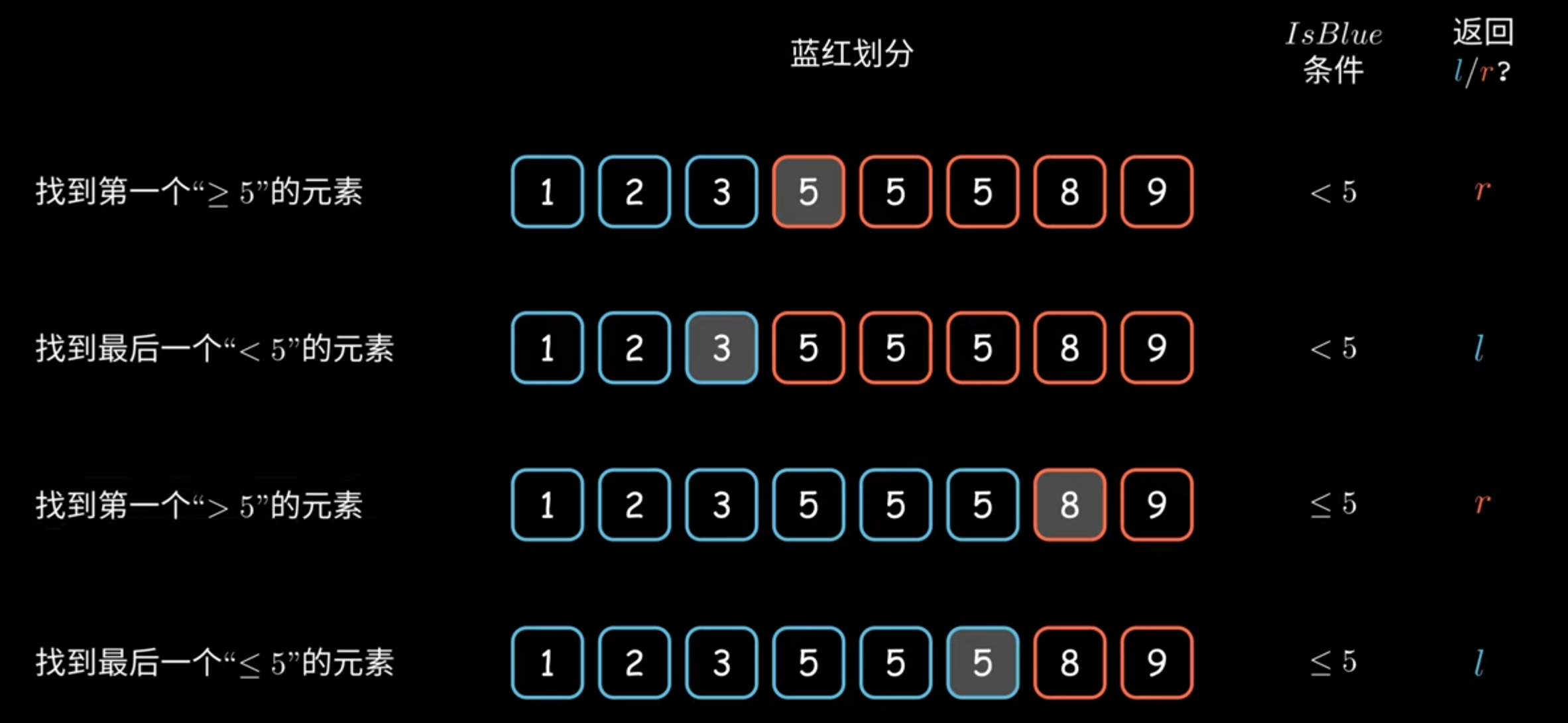
  • 找到第一个">=5"的元素
  • 找到最后一个"<=5"的元素
  • 找到最后一个"<5"的元素
  • 找到第一个">5"的元素

这4个问题表面上相似，但细节上却有不同，用二分查找细节处理并不容易。

红蓝边界法 #

初始列表可以全部视为灰色，目标将列表分为红蓝两部分区域：

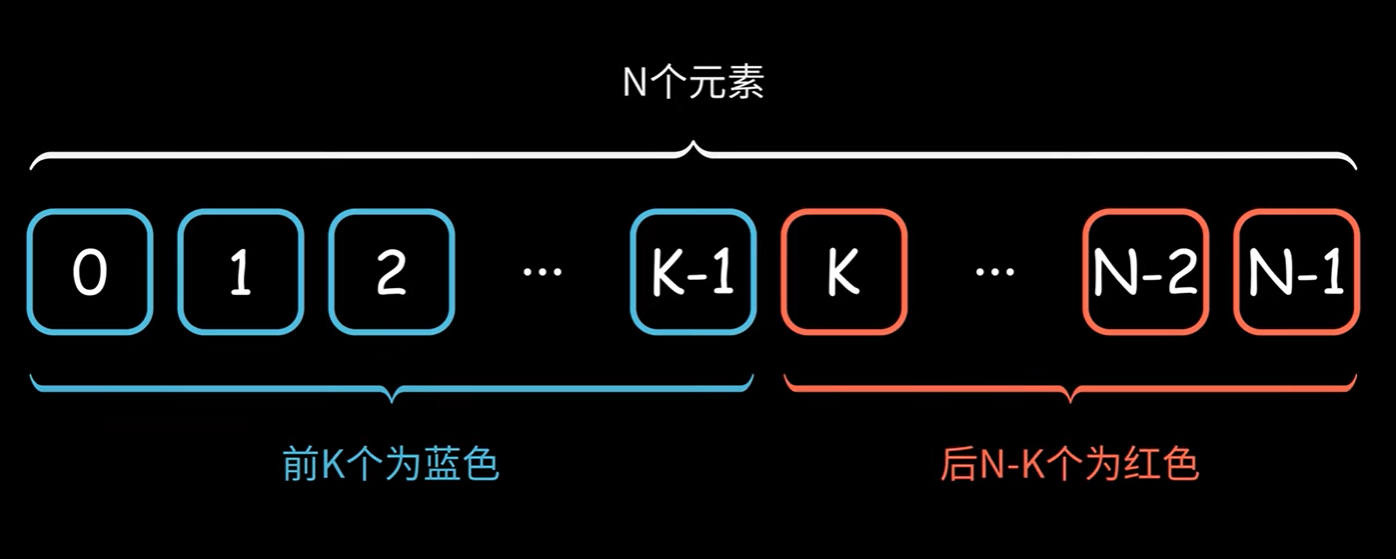
l,r 分别指向红蓝区域边界，根据题目要求赋予红蓝区域特定含义，并不断调整红蓝区域边界：

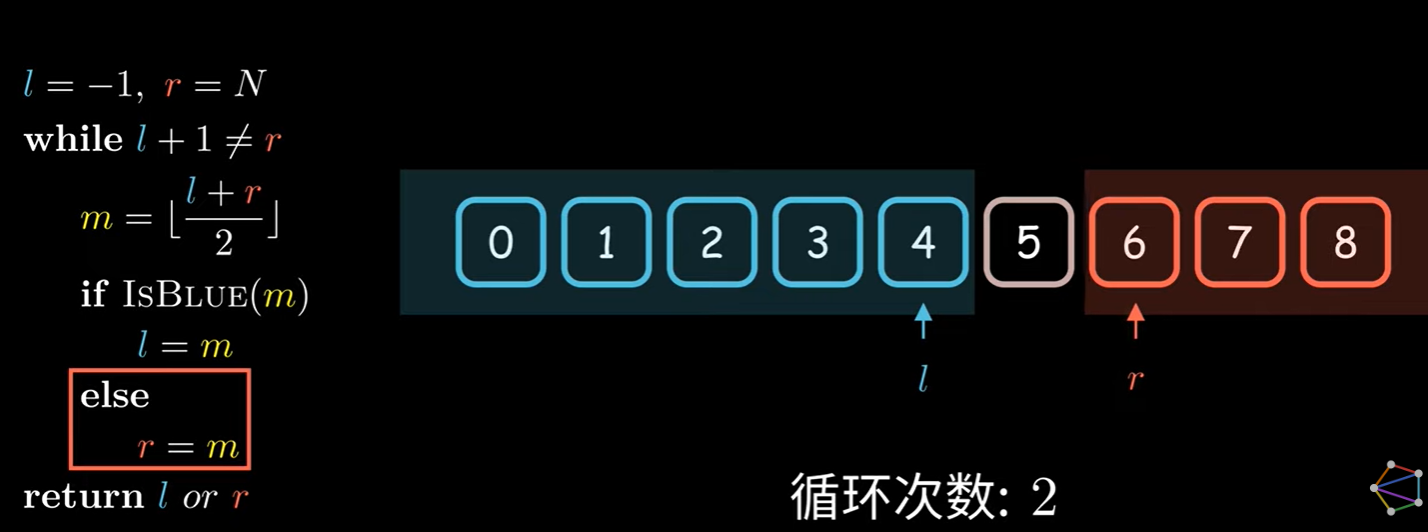
根据题目要求返回 l,r

细节问题 #

细节1：为什么l的初始值为-1，r的初始值为N？

答：因为整个数组可能最终是全红或者全蓝，违反了我们对l,r的定义，继而引起错误。

细节2：m是否始终处于[0,N)以内？

答：基于循环条件l+1 ≠ r，可得l,r的最值，进而判断m始终处于[0,N)以内。

细节3：更新指针时，能不能像常规的二分查找那样，能不能写成 l=m+1，或者 r=m-1？

答：不能。可能会导致l指向红色区域，或者r指向蓝色区域，违反了我们对l,r的定义，继而引起错误。

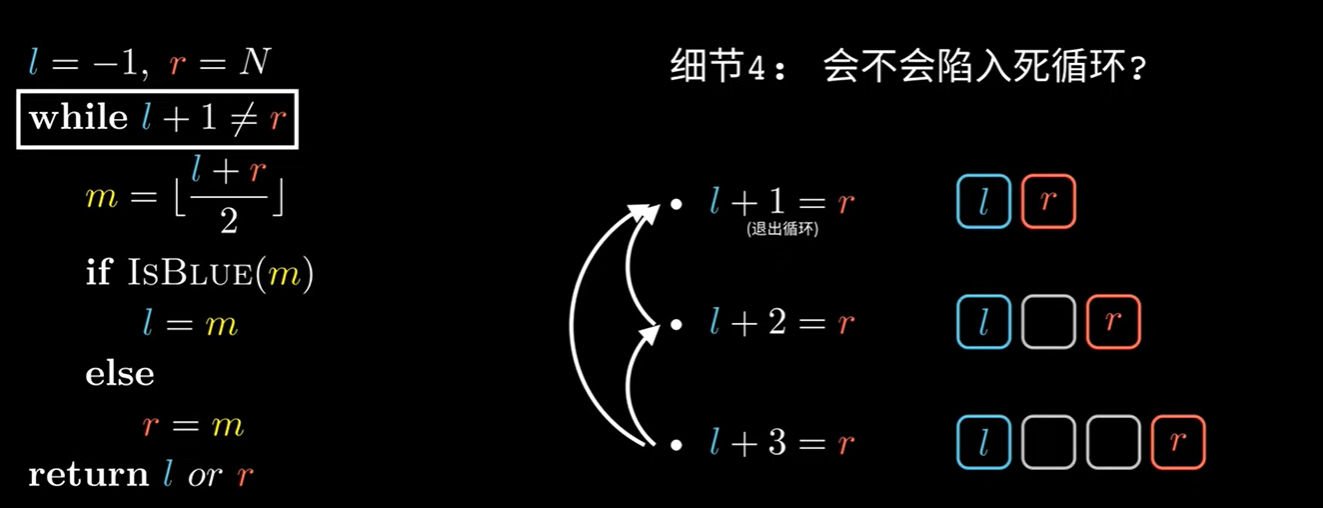
细节4：程序会不会陷入死循环？

答：不会。不论l,r的值为多少，都会回归到l+1=r，这种情况。

答案 #

求平方根 #

这里想通过二分查找求平方根来表达，二分查找的解决对象重要的是满足单调性，而不限于离散型有序数组、整数下表等。

  1. 确定初始区间：为目标数\(a\)（\(a\ge 0\)）设定一个初始的搜索区间。如果\(a\ge 1\)，一个合适的区间是\([0,a]\)；如果\(0\le a<1\)，则区间应为\([0,1]\)。综合起来，一个安全的选择是\([0,\max (1,a)]\)。
  2. 计算中点：计算当前区间的中间值，\(mid=(low+high)/2\)。
  3. 检查中点的平方：
  • 如果 \(mid^2\) 非常接近\(a\)（在预设的精度范围内），则 \(mid\) 就是我们需要的平方根
  • 如果\( mid^{2} \lt a \)，说明 \(a\) 的平方根应该在区间\([mid, high]\)内，所以将\(low\)更新为\(mid\)
  • 如果\(mid^{2} \gt a\)，说明 \(a\) 的平方根应该在区间\([low, mid]\)内，所以将\(high\)更新为\(mid\)
  1. 重复过程：重复步骤2和3，每次都将搜索区间缩小一半，直到满足预设的精度要求为止
Edit Edit this page