定义 #
在理解定义之前,先看一下来自 Quora 接近50k的回复:
在一张纸上写下: 1+1+1+1+1+1+1+1 =
上面等式等于多少: 数了数,发现有8个1,等于 8
如果在上述等式的左边再写:1+
现在等式等于几?能够快速回答等于 9
是怎么能够快速算出来等于 9 的 ?因为原来是等于8,你只是额外加了 1,不用重复的去数
动态规划(Dynamic programming,简称DP)是一种将复杂问题分解成很多子问题(具备最优子结构),并将子问题的求解结果存储起来避免重复求解(子问题重叠)节省时间的一种算法。
多数情况下它可以采用自下而上的递推方式来得出每个子问题的最优解(即最优子结构),子问题之间是有一定联系的,通过状态转移方程,进而自然而然地得出依赖子问题的原问题的最优解。
简单总结一下,最优子结构,状态转移方程,重叠子问题就是动态规划的三要素,这其中定义子问题的状态(DP 状态)与写出状态转移方程是解决动态规划最为关键的步骤,解决了这些动态规划就基本不是问题了。
题目 #
求解动态规划基本思路如下(解题四步曲):
- 判断是否可用递归来解,可以的话进入步骤 2 - 说明存在最优子结构
- 分析在递归的过程中是否存在大量的重复子问题 - 存在重叠子问题
- 采用备忘录的方式来存子问题的解以避免大量的重复计算
- 改用自底向上的方式来递推 - 找到状态转移方程
斐波那契数列 #
斐波那契数列的定义可以用递推公式表示: \(F(0)=0\) ,\(F(1)=1\), \(F(n)=F(n-1)+F(n-2)\) (其中 \(n\ge 2\))
看看怎么用动态规划解题四步曲来解斐波那契数列:
- 判断是否可用递归来解
def fibonacci(n):
if n == 1:
return 1
if n == 2:
return 2
return fibonacci(n - 1) + fibonacci(n - 2)
- 分析在递归的过程中是否存在大量的重复子问题 - 画出递归树
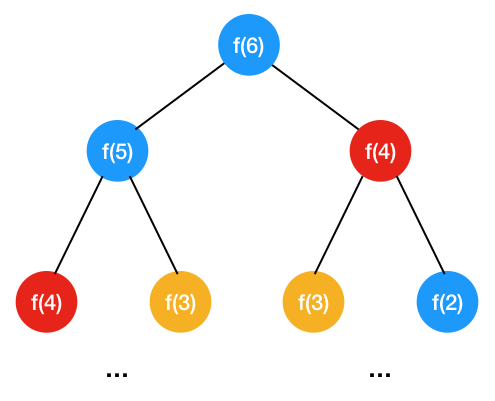
可以看到存在重复计算的情况,大致能够看出此递归的时间复杂度是质数级别的
- 采用备忘录的方式来存子问题的解以避免大量的重复计算
memo = {}
def fibonacci(n):
if n == 1:
return 1
if n == 2:
return 2
if n in memo:
return memo[n]
result = fibonacci(n - 1) + fibonacci(n - 2)
memo[n] = result
return result
缓存之后对应的递归树
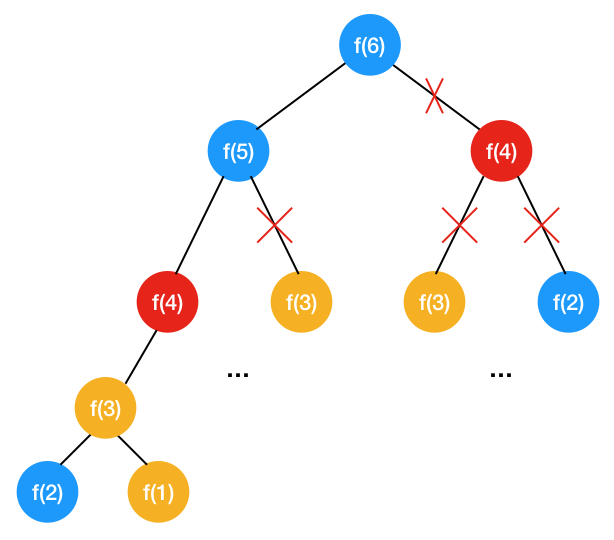
可以看到通过缓存中间的数据,做了大量地剪枝的工作,避免了重复计算,时间复杂度变成了 O(n)
- 改用自底向上的方式来递推
有以下规律:
f(1) = 1
f(2) = 2
f(3) = f(1) + f(2) = 3
f(4) = f(3) + f(2) = 5
....
f(n) = f(n-1) + f(n-2)
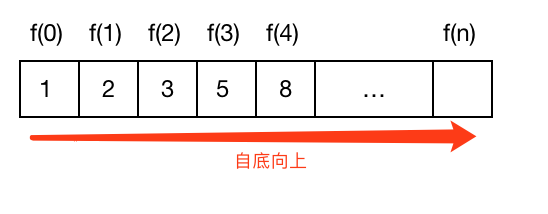
f(n) 就是定义的每个子问题的状态(DP 状态),f(n) = f(n-1) + f(n-2) 就是状态转移方程,即 f(n) 由 f(n-1), f(n-2) 这两个状态转移而来,由于每个子问题只与它前面的两个状态有关,所以我们只要定义三个变量,自底向上不断循环迭代即可
def f(n):
if n == 1:
return 1
if n == 2:
return 2
result = 0
pre = 1
next_val = 2
for i in range(3, n + 1):
result = pre + next_val
pre = next_val
next_val = result
return result
斐波那契数列并不是严格意义上的动态规划,并不涉及最优子结构,只是先用这个简单地例子来帮助大家了解一下一些基本的概念:自底向上,DP 状态, 状态 转移方程
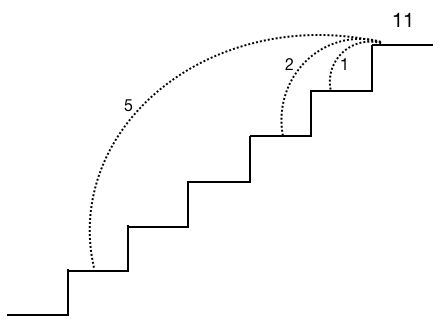
三角形的最小路径和 #
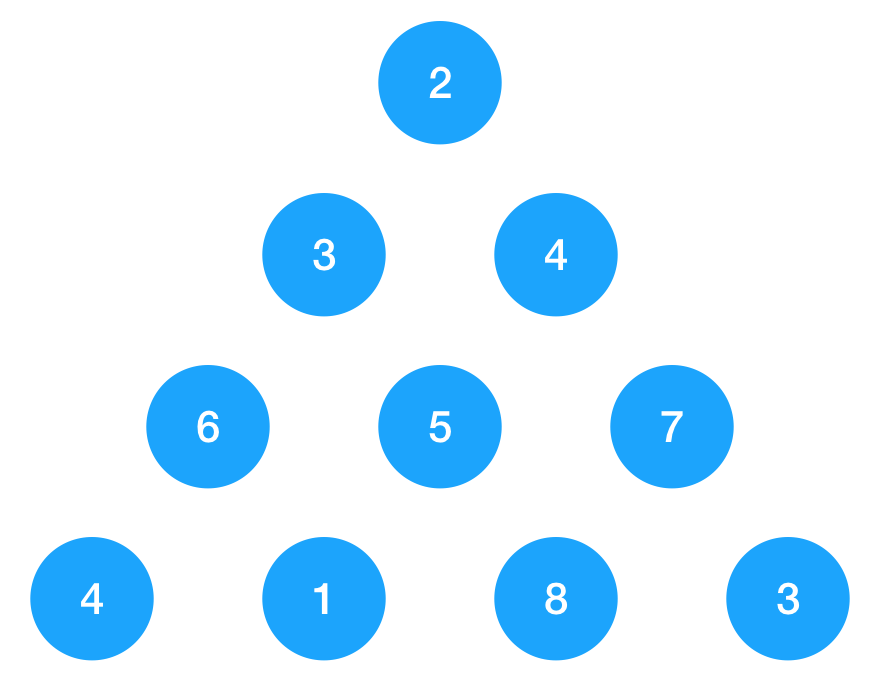
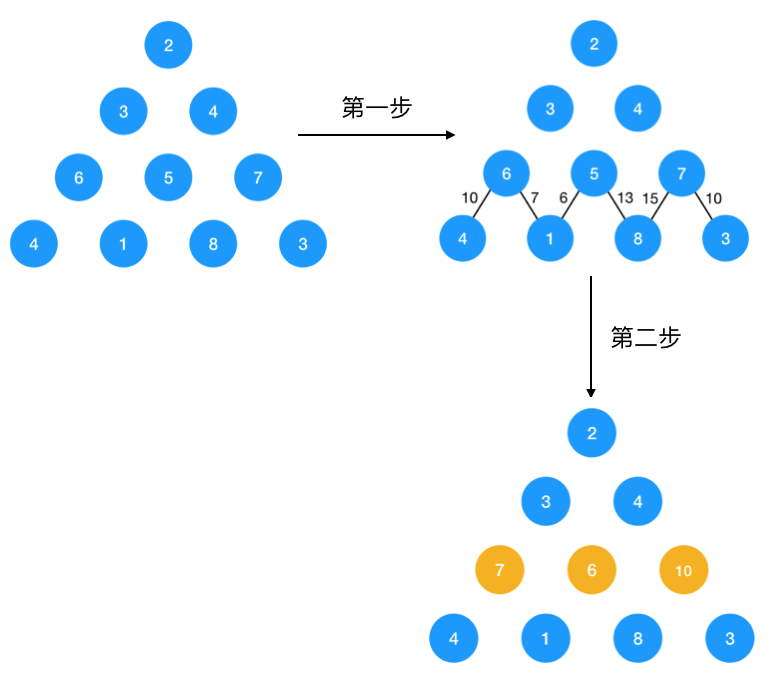
如图示,以上三角形由一连串的数字构成,要求从顶点 2 开始走到最底下边的最短路径,每次只能向当前节点下面的两个节点走,如 3 可以向 6 或 5 走,不能直接走到 7。
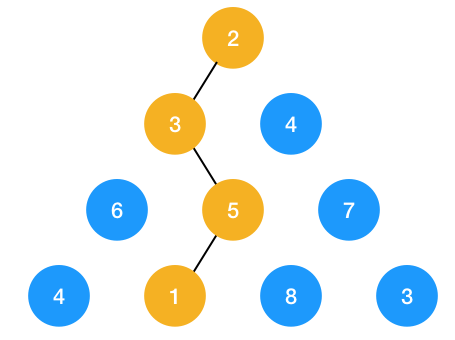
如图示,从 2 走到最底下最短路径为 2+3+5+1 = 11,即为我们所求的结果。
首先我们需要用一个二维数组来表示这个三个角形的节点,用二维数组显然可以做到,第一行的 2 用 a[0][0] 表示,第二行元素 3, 4 分别用 a[1][0],a[1][1],依此类推。
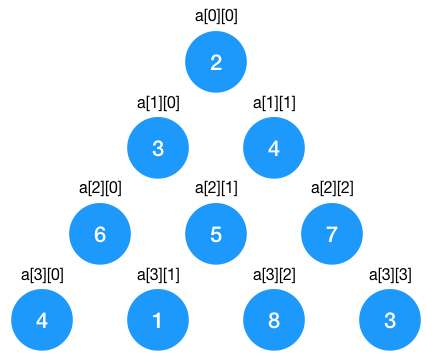
套用动态规划解题套路来解题
- 判断是否可用递归来解
假设我们定义 traverse(i, j) 为遍历节点a[i][j],每个节点都可以走它的左下或右下节点,则可以得出递归公式的代码如下:
traverse(i, j) = {
traverse(i+1, j); 向节点i,j 下面的左节点走一步
traverse(i+1, j+1); 向节点i,j 下面的右节点走一步
}
遍历到三角形最后一条边的节点时终止,对每个节点来说,在往下遍历的过程中,问题规模不断地在缩小。
完整递归代码如下:
triangle = [
[2, 0, 0, 0],
[3, 4, 0, 0],
[6, 5, 7, 0],
[4, 1, 8, 3]
]
total_row = 4 # 总行数
def traverse(i, j):
if i >= total_row - 1:
return 0
# 往左下节点走
left_sum = traverse(i + 1, j) + triangle[i + 1][j]
# 往右下节点走
right_sum = traverse(i + 1, j + 1) + triangle[i + 1][j + 1]
# 返回较小的路径和
return min(left_sum, right_sum)
对于每个节点,要么向左或向右,每个问题都分解成了两个子问题,和斐波那契数列一样,如果画出递归树也是个二叉树,所以时间复杂度是 O(2^n),也是指数级别。
- 分析在递归的过程中是否存在大量的重复子问题
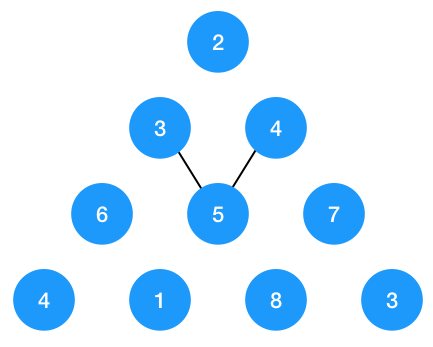
对于节点 3 和 4 来说,如果节点 3 往右遍历, 节点 4 往左遍历,都到了节点 5,节点 5 往下遍历的话就会遍历两次,所以此时就会出现重复子问题
- 采用备忘录的方式来存子问题的解以避免大量的重复计算
triangle = [
[2, 0, 0, 0],
[3, 4, 0, 0],
[6, 5, 7, 0],
[4, 1, 8, 3]
]
# 记录中间状态的字典
memo = {}
def traverse(i, j):
key = f"{i},{j}" # 用字符串作为键
if key in memo:
return memo[key]
# 到达最后一行
if i == len(triangle) - 1:
return triangle[i][j]
# 往左下节点走
left_sum = traverse(i + 1, j)
# 往右下节点走
right_sum = traverse(i + 1, j + 1)
# 取最小路径和
result = triangle[i][j] + min(left_sum, right_sum)
memo[key] = result
return result
时间复杂度下降到了 O(n)
- 改用自底向上的方式来递推
要求节点 2 到底部边的最短路径,只要先求得节点 3 和 节点 4 到底部的最短路径值,然后取这两者之中的最小值再加 2 ,就是从 2 到底部的最短路径了;同理类推,一直到最后一层,到底部的最短路径就是其本身。所以问题转换为了,已知最后一层节点的最小值,怎么求倒数第二层到底部的最小值,直到第一层节点到底部的最小值。
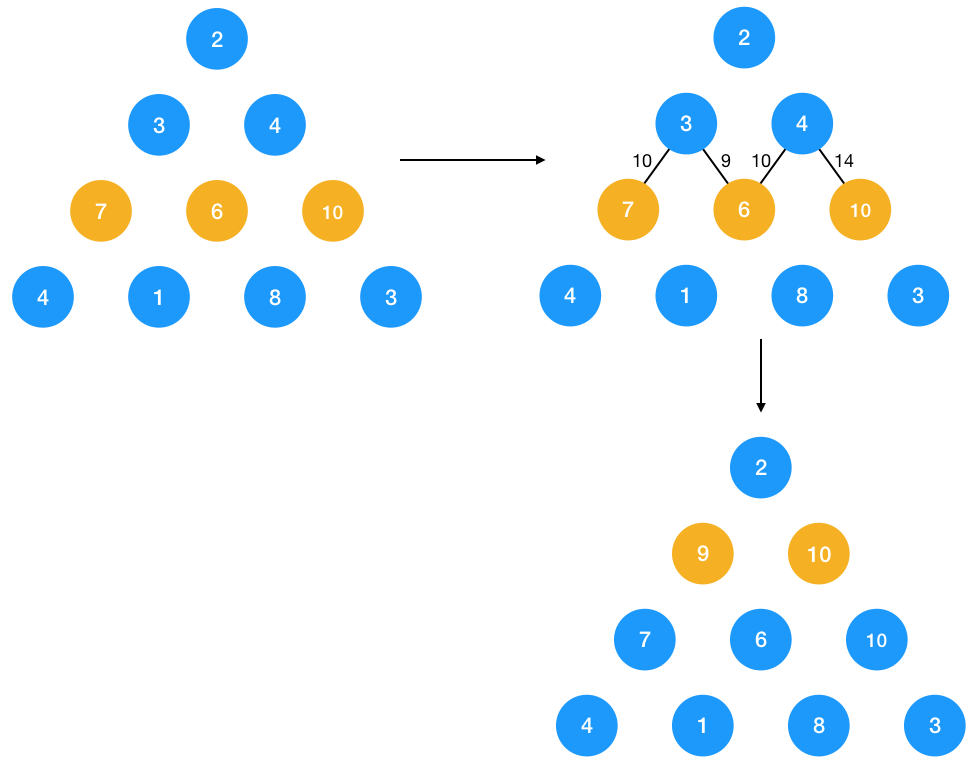
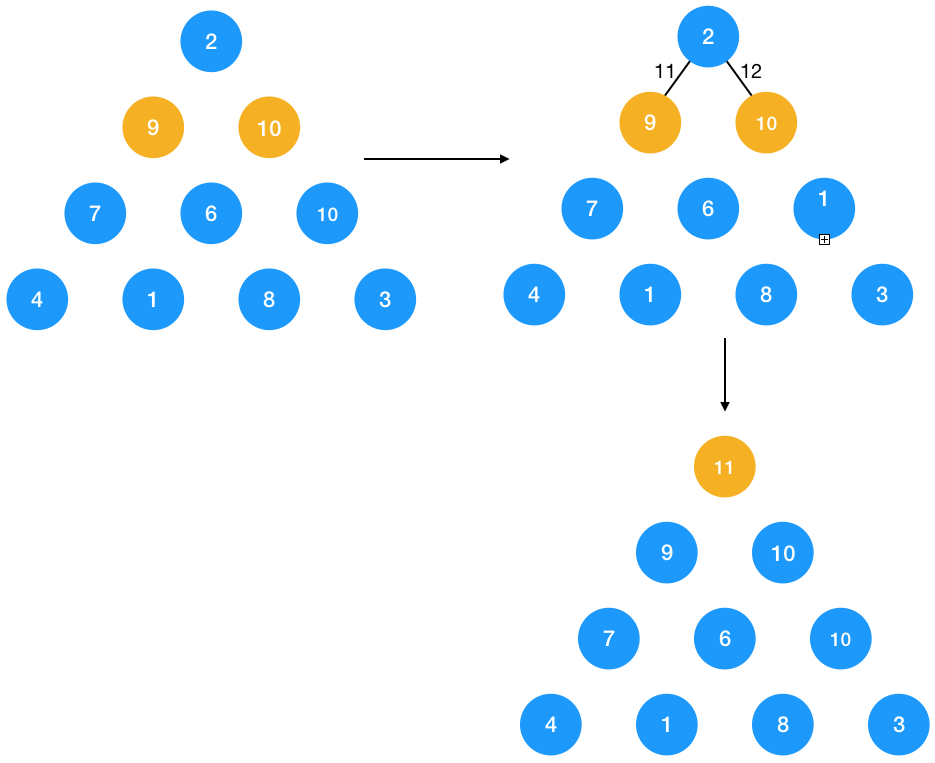
最终的 11 即为我们所求的值,来看看怎么定义 DP 的状态与状态转移方程,要求每个节点到底部的最短路径,于是 DP 状态 DP[i,j] 定义为 i,j 的节点到底部的最小值,DP状态转移方程定义如下:
DP[i,j] = min(DP[i+1,j], DP[i+1,j+1]) + triangle[i][j]
# 可以看出上层的结果依靠下层,所以从下层往上层递推
triangle = [
[2, 0, 0, 0],
[3, 4, 0, 0],
[6, 5, 7, 0],
[4, 1, 8, 3]
]
n = len(triangle)
dp = [[0 for _ in range(n)] for _ in range(n)]
dp[n-1] = triangle[n-1]
for i in range(n-2,-1,-1):
for j in range(0,n-1):
dp[i][j] = min(dp[i+1][j], dp[i+1][j+1]) + triangle[i][j]
print(dp[0][0]) # 11
我们知道每个节点到底部的最短路径只与它下一层的 DP[i+1,j], DP[i+1,j+1] 有关,即每一层的最短路径得出后,下层的结果就不需要报错了,我们可以尝试将每一层节点的 DP[i,j] 保存到一个一维数组里,每一层的结果都保存在这个一维数组里,从而达到存储空间的优化。
triangle = [
[2, 0, 0, 0],
[3, 4, 0, 0],
[6, 5, 7, 0],
[4, 1, 8, 3]
]
n = len(triangle)
dp = triangle[n-1]
for i in range(n-2,-1,-1):
for j in range(0,i+1):
dp[j] = min(dp[j], dp[j+1]) + triangle[i][j]
print(dp[0]) # 11
凑零钱 #
给定不同面额的硬币,用coins数组表示,和一个总金额 amount。编写一个函数来计算正好凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
如:
- 输入:
coins = [1, 2, 5],amount = 11,输出: 3,解释:11 = 5 + 5 + 1 - 输入:
coins = [2],amount = 3,输出: -1
- 判断是否可用递归来解
假设我们定义count[sum]为正好凑成总金额为sum时所需的最少硬币个数,则count[sum] = min(count[sum], count[sum-coins] + 1)
def count(sum):
if sum == 0:
return 0
if sum < 0:
return -1
res = 99999
for i in range(len(coins)):
sub = count(sum-coins[i])
if sub == -1:
continue
res = min(res, sub+1)
if res == 99999:
return -1
return res
coins = [1, 2, 5]
print(count(11)) # 3
- 分析在递归的过程中是否存在大量的重复子问题
针对 amount = 11 的递归树如下
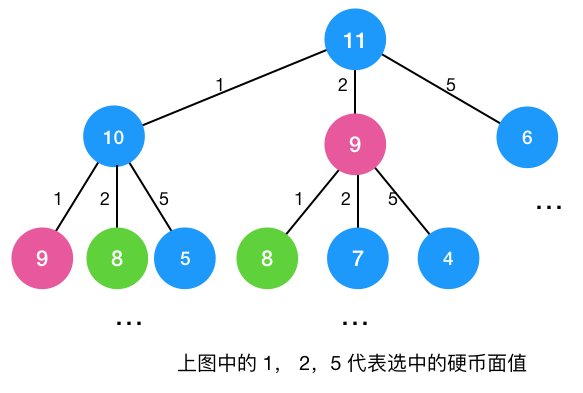
发现有重复计算的问题,存在重叠子问题,且凑零钱的递归树是一颗n叉树(看硬币的数量),显然时间复杂度也是指数级别
- 采用备忘录的方式来存子问题的解以避免大量的重复计算
memo = {}
def count(sum):
if sum in memo:
return memo[sum]
if sum == 0:
return 0
if sum < 0:
return -1
res = 99999
for i in range(len(coins)):
sub = count(sum-coins[i])
if sub == -1:
continue
res = min(res, sub+1)
if res == 99999:
memo[sum] = res
return -1
memo[sum] = res
return res
coins = [1, 2, 5]
print(count(11)) # 3
- 改用自底向上的方式来递推
sum = 11
coins = [1, 2, 5]
def exchange(sum, coins):
dp = [99999 for i in range(sum+1)]
for c in coins:
dp[c] = 1
for i in range(0, sum+1):
for c in coins:
dp[i] = min(dp[i], dp[i-c]+1)
if dp[i] == 99999:
return -1
return dp[i]
print(exchange(sum, coins))
凑零钱这道题还可以用另外一道经典的青蛙跳台阶的思路来考虑:从最底部最少跳多少步可以跳到第 11 阶,一次可以跳 1,2,5步。
由此可知最后一步一定是跳 1 或 2 或 5 步,于是如果用
f(n)代表跳台阶 n 的最小跳数,则问题转化为了求f(n-1),f(n-2),f(n-5)的最小值。递推表达式:
f(n) = min{ f(n-1),f(n-2),f(n-5)} + 1 (1代表最后一跳)
以上只是求出了凑成零钱的的最小数量,但如果想求由哪些面值的硬币构成的,该如何修改呢?