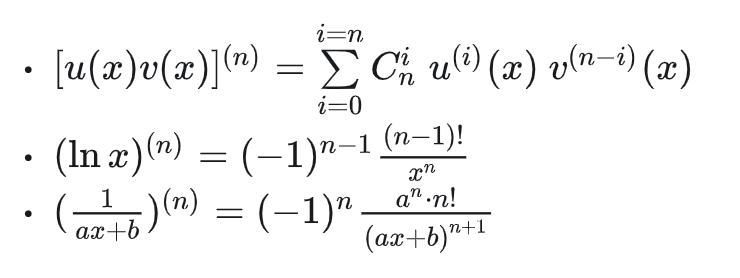定义 #
如果 \(\lim_{\Delta x\to0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\) 存在,那么称函数 \(f(x)\) 在 \(x=x_0\) 处的可导,导数也称为微商,记为\(\frac{df(x)}{dx}或y'\)
等价形式:\(\lim_{x\to x_0}\frac{f(x) - f(x_0)}{x - x_0}\)
左导数:\(f'_{-}(x_0) = \lim_{\Delta x\to0^-}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} \) 右导数:\(f'_{+}(x_0) = \lim_{\Delta x\to0^+}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} \)
导数存在的充要条件: 左右导数存在,且\(f'_{-}(x_0) = f'_{+}(x_0)\)
各种意义 #
几何意义:函数曲线在该点处切线的斜率
例如函数 \(f(x)=x^2\),在 \(x=2\) 处导数为 \(f'(2)=4\),意味着函数曲线 \(f(x)=x^2\) 在点\((2,4)\) 处的切线斜率为4
物理意义:函数在该点处的瞬时变化率
例如函数 \(f(t)\) 表示物体在时间 \(t\) 处的位移,那么 \(f'(t)\) 表示物体在时间 \(t\) 处的瞬时速度
求导公式 #
$$ \begin{align*} & (x^n)' = nx^{n-1} \\ & (e^x)' = e^x \\ & (\log_ax)' = \frac{1}{x \ln a}(a>0且a≠1,x>0),特别地,(\ln x)' = \frac{1}{x} \\ & (\sin x)' = \cos x, (\cos x)' = -\sin x \\ & (\tan x)' = \sec x^2, (\cot x)' = -\csc x^2 \\ & (\arcsin x)' = \frac{1}{\sqrt{1-x^2}},(\arccos x)' = -\frac{1}{\sqrt{1-x^2}}, (\arctan x)' = \frac{1}{1+x^2} , (arccotx)' = -\frac{1}{1+x^2} \\ \end{align*} $$ $$ \begin{align*} & 复合函数求导:[f(g(x))]' = f'(g(x))\cdot g'(x) \\ & 积法则:(uv)' = u'v + v'u 可推广到n个函数的乘积\\ & 商法则:(\frac{u}{v})' = \frac{u'v-v'u}{v^2} \\ & \\ & 链式法则:如果u=g(x)在x点可导,而y=f(u)在u=g(x)点可导,那么复合函数y=f[g(x)]在x点可导,其导数为:\\ & \frac{dy}{dx} = f'(u)g'(x) 或 \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} \\ & \\ & 参数方程求导:x=f(t), y=g(t)是由参数t表示的函数,则(\frac{dy}{dx})' = \frac{g'(t)}{f'(t)} \\ \end{align*} $$ $$ 反函数求导:反函数的导数等于其直接函数导数的倒数,\frac{dy}{dx} = \frac{1}{\frac{dx}{dy}} 或 [f^{-1}(x)]' = \frac{1}{f'(y)}(关于y=x对称的体现) $$ $$ 多元函数的偏导数:设z=f(x,y),则它的偏导数f'_x= \frac{\partial z}{\partial x}(y视为常数),f'_y= \frac{\partial z}{\partial y}(x视为常数) $$ $$ \begin{align*} & 多元复合函数求导:如果函数 x=\varphi(t) 和 y=\psi(t) 都在t_0点可导,函数 z=f(x,y) 在 t_0 点对应的 (x_0,y_0) 点有连续的偏导数,\\ & 那么复合函数 z=f[\varphi(t),\psi(t)] 在 t_0 点可导,且有( t_0 实际上代表了任意 t,所以下面省略了 |_{t=t_0}):\\ & \frac{dz}{dt}=\frac{\partial z}{dx}\cdot\frac{\partial x}{dt} + \frac{\partial z}{\partial y}\cdot\frac{dy}{dt} \\ & 其中\frac{\mathrm{d}z}{\mathrm{d}t}也被称为全导数。对比单变量函数的链式法则,上述定理就是多元函数的链式法则。 \end{align*} $$ $$ \begin{align*} & 隐函数求导:F(x,y) = 0,降y = f(x) 代入,得 \\ & F(x, f(x)) = 0 \\ & 左边看作是x,y的多元复合函数,求这个函数的全导数。等式两边同时求导,等式仍然成立,得 \\ & \frac{\partial F}{\partial x}+\frac{\partial F}{\partial y}\cdot\frac{dy}{dx} = 0 \\ & 由于F_y'连续且F_y'(x_0,y_0) \ne 0,所以存在(x_0,y_0)的一个去心邻域,在这个邻域内F_y' \ne 0,得 \\ & \frac{dy}{dx} = - \frac{F_x'}{F_y'} \end{align*} $$ $$ \begin{align*} & 变限积分求导:\\ & (1)下限为常数,上限为函数类型:y= \int_a^{f(x)}g(t)dt \\ & y' = g(f(x))d(f(x)) = g(f(x))f'(x) \\ & 例如 y = \int_1^{x^2}e^{t^2}dt \\ & y' = e^{x^4}d(x^2) = 2x \cdot e^{x^4} & \\ & (2)下限为函数,上限为常数类型:与第一种相差负号 \\ & (3)上下限均为函数类型:y = \int_{h(x)}^{g(x)}f(t)dt \\ & y = \int_{h(x)}^{g(x)}f(t)dt = \int_{0}^{g(x)}f(t)dt + \int_{h(x)}^{0}f(t)dt = \\ & \int_{0}^{g(x)}f(t)dt - \int_{0}^{h(x)}f(t)dt = f(g(x))g'(x) - f(h(x))h'(x) \\ & 例如 y=\int_{x^2}^{x^3}e^tdt \\ & y' = 3x^2e^{x^3}- 2xe^{x^2} \end{align*} $$- 奇函数的导数是偶函数
- 偶函数的导数是奇函数
- 周期函数求导不改变周期大小
高阶导数 #
$$ \begin{align*} 函数y=f(x)在点(x_0,y_0)处的二阶导数为f''(x_0) = \lim_{\Delta x \to x}\frac{f'(x_0+\Delta x)-f'(x_0)}{\Delta x} \\ 或 f''(x_0) = \lim_{x \to x_0}\frac{f'(x)-f'(x_0)}{x-x_0} \\ \\ 函数y=f(x)在点(x_0,y_0)处的n(n\ge2,n\in\mathbb{Z})阶导数为f^n(x_0) = \lim_{\Delta x \to x}\frac{f^{n-1}(x_0+\Delta x)-f^{n-1}(x_0)}{\Delta x} \\ 或 f^n(x_0) = \lim_{x \to x_0}\frac{f^{n-1}(x)-f^{n-1}(x_0)}{x-x_0} \\ \\ y'',y''',y^{(4)},...,y^{(n)} 或者 \\ \frac{d^2y}{dx^2},\frac{d^3y}{dx^3},\frac{d^4y}{dx^4},...,\frac{d^ny}{dx^n} = \frac{d(\frac{d^{n-1}y}{dx^{n-1}})}{dx} \end{align*} $$公式,第一个为莱布尼茨公式