幂函数 #
\[ f(x) = x^a \quad \text{for } a \in \mathbb{R} \]利用恒等变形(即换底变形)\([f(x)]^{g(x)} = e^{g(x) \ln f(x)}\) 及复合函数 \(e^{u(x)}\) 求极限法则 \(\lim_{x \to *} e^{u(x)} = e^{\lim_{x \to *} u(x)}\),有
\[ \lim_{x \to *} \left[ f(x) \right]^{g(x)} = e^{\lim_{x \to *} [g(x) \ln f(x)]} \]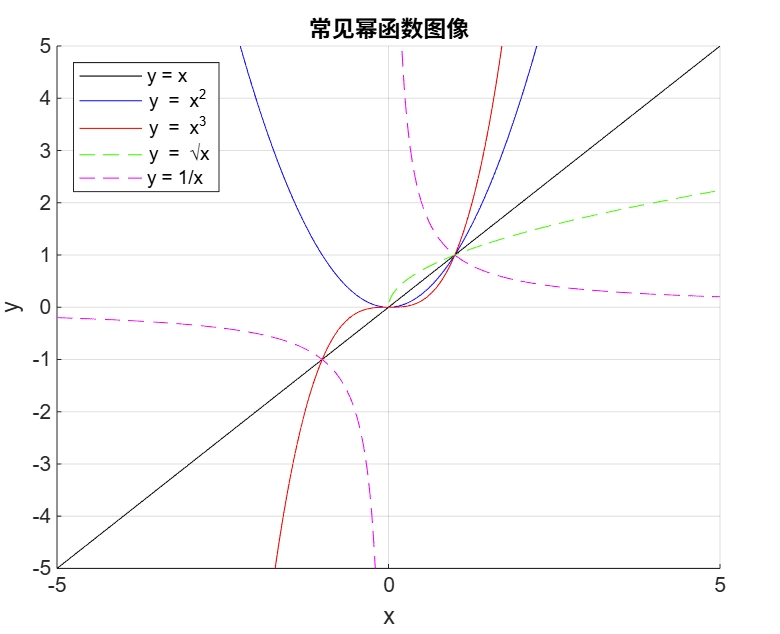
指数函数 #
\[ f(x) = a^x \quad \text{for } a > 0, a \neq 1 \]指数运算法则
\[ a^\alpha \cdot a^\beta = a^{\alpha+\beta},\frac{a^\alpha}{b^\beta} = a^{\alpha-\beta}, (a^\alpha)^\beta = {a^\alpha}^\beta, (ab)^\alpha = a^\alpha b^\alpha, (\frac{a}{b})^\alpha = \frac{a^\alpha}{b^\alpha} \quad 其中a,b是正实数,\alpha,\beta是任意实数 \]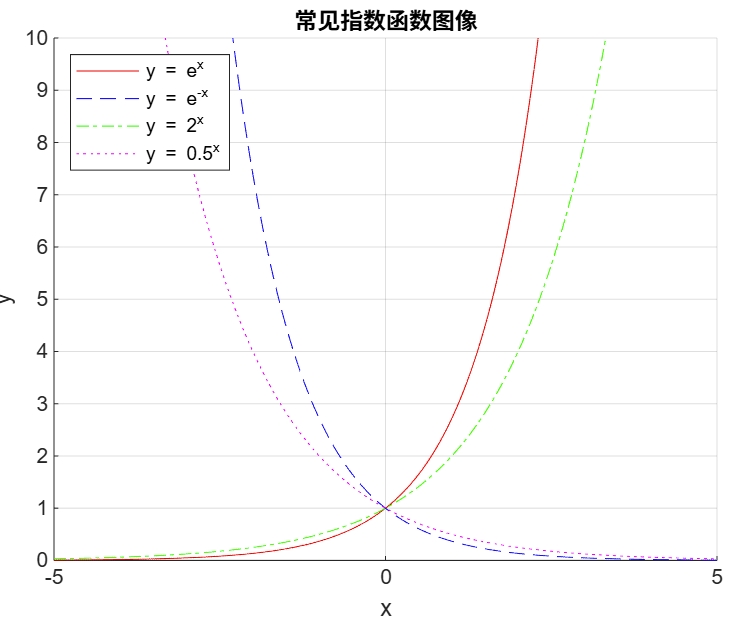
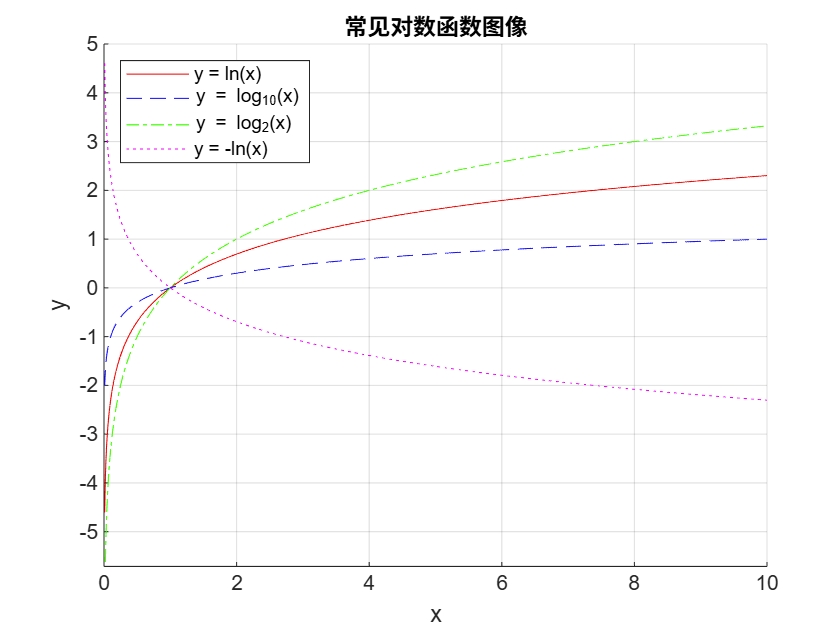
对数函数 #
\[ f(x) = \log_a x \quad \text{for } a > 0, a \neq 1 \\ \]对数运算法则
积的对数=对数的和 \(\log_a(MN) = \log_aM + \log_aN \)
商的对数=对数的差 \(\log_a\frac{M}{N} = \log_aM - \log_aN \)
幂的对数=对数的倍数
三角函数 #
\[ \begin{aligned} \sin(x) \text{正弦} \\ \cos(x) \text{余弦} \\ \tan(x) \text{正切} \\ \csc(x) = \frac{1}{\sin(x)} \text{余割} \\ \sec(x) = \frac{1}{\cos(x)} \text{正割} \\ \cot(x) = \frac{1}{\tan(x)} \text{余切} \end{aligned} \]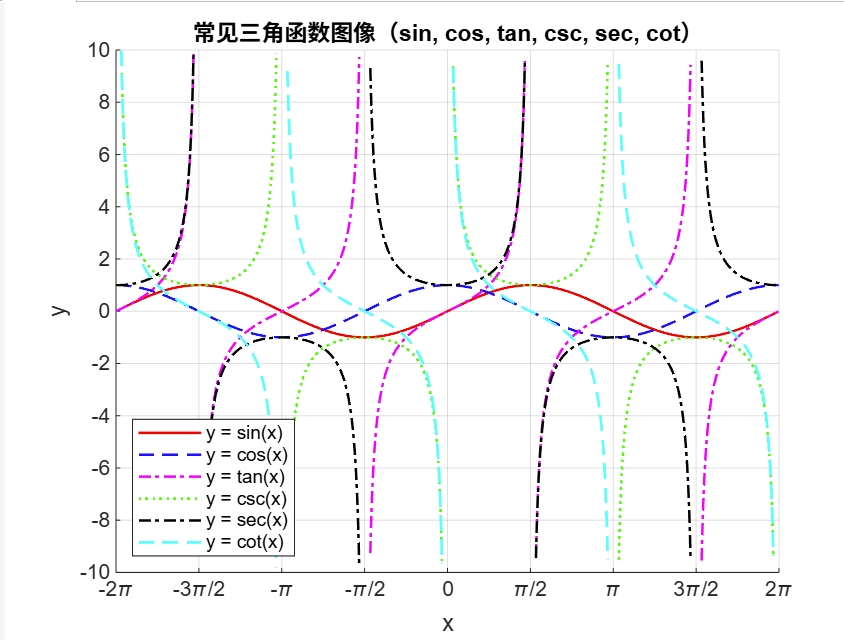
反三角函数 #
\[ \begin{aligned} \arcsin(x) \text{反正弦} \\ \arccos(x) \text{反余弦} \\ \arctan(x) = \frac{\pi}{2} - \text{arccot(x)} \text{反正切} \end{aligned} \]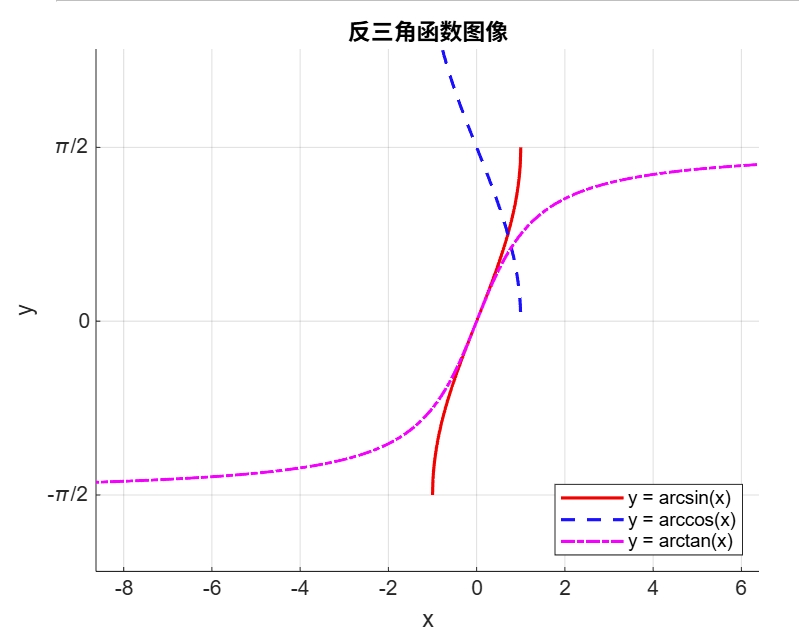
三角函数的基本关系 #
\[ \tan a = \frac{\sin a}{\cos a}, \quad \csc a = \frac{1}{\sin a}, \quad \sec a = \frac{1}{\cos a}, \quad \cot a = \frac{1}{\tan a}, \quad \sin^2a + \cos^2a = 1, \quad 1 + \tan^2a = \sec^2a, \quad 1 + \cot^2a = \csc^2a \]三角函数重要公式 #
诱导公式:奇变偶不变,符号看象限
奇偶指的是 \(\frac{\pi}{2}\) 倍数的奇偶(这个影响 \(x,y\) 坐标是怎么变换的),象限值得是将 \(\alpha\) 视为锐角,并加上对应弧度,原三角函数所在象限对应的符号,如
倍角公式
\[ \begin{align} \sin2\alpha = 2\sin\alpha\cos\alpha ,\cos2\alpha = \cos^2\alpha - \sin^2\alpha = 1 - 2\sin^2\alpha = 2\cos^2\alpha - 1 \\ \sin3\alpha = -4\sin^3\alpha + 3\sin\alpha, \cos3\alpha = 4\cos^3\alpha - 3\cos\alpha \\ \tan2\alpha = \frac{2\tan\alpha}{1 - \tan^2\alpha}, \cot2\alpha = \frac{\cot^2\alpha - 1}{2\cot\alpha} \end{align} \]半角公式
\[ \begin{align} \sin^2\frac{\alpha}{2} = \frac{1}{2}(1 - \cos\alpha) \\ \cos^2\frac{\alpha}{2} = \frac{1}{2}(1 + \cos\alpha) \end{align} \]降幂公式
\[ \begin{align} \sin\frac{\alpha}{2} = \pm \sqrt{\frac{1}{2}(1 - \cos\alpha)}, \quad \cos\frac{\alpha}{2} = \pm \sqrt{\frac{1}{2}(1 + \cos\alpha)}, \\ \tan\frac{\alpha}{2} = \frac{1 - \cos\alpha}{\sin\alpha} = \frac{\sin\alpha}{1 + \cos\alpha} = \pm \sqrt{\frac{1 - \cos\alpha}{1 + \cos\alpha}}, \\ \cot\frac{\alpha}{2} = \frac{\sin\alpha}{1 - \cos\alpha} = \frac{1 + \cos\alpha}{\sin\alpha} = \pm \sqrt{\frac{1 + \cos\alpha}{1 - \cos\alpha}}\\ \\ \end{align} \]和差公式
\[ \begin{align} \sin(\alpha \pm \beta) = \sin\alpha \cos\beta + \cos\alpha\sin\beta, \quad \cos(\alpha \pm \beta) = \cos\alpha\cos\beta \mp \sin\alpha\sin\beta,\\ \tan(\alpha \pm \beta) = \frac{\tan\alpha \pm \tan\beta}{1 \mp \tan\alpha\tan\beta}, \quad \cot(\alpha \pm \beta) = \frac{\cot\alpha\cot\beta \mp 1}{\cot\beta \pm \cot\alpha}\\ \end{align} \]积化和差与和差化积
\[ \begin{align} \sin\alpha\cos\beta = \frac{1}{2}[\sin(\alpha+\beta)+\sin(\alpha-\beta)], \cos\alpha\sin\beta = \frac{1}{2}[\sin(\alpha+\beta)-\sin(\alpha-\beta)],\\ \cos\alpha\cos\beta = \frac{1}{2}[\cos(\alpha+\beta)+\cos(\alpha-\beta)], \sin\alpha\sin\beta = \frac{1}{2}[\cos(\alpha-\beta)-\cos(\alpha+\beta)],\\ \sin\alpha+\sin\beta = 2\sin\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}, \sin\alpha-\sin\beta = 2\sin\frac{\alpha-\beta}{2}\cos\frac{\alpha+\beta}{2},\\ \sin\alpha-\sin\beta = 2\sin\frac{\alpha-\beta}{2}\cos\frac{\alpha+\beta}{2}, \sin\alpha-\sin\beta = 2\sin\frac{\alpha-\beta}{2}\cos\frac{\alpha+\beta}{2},\\ \cos\alpha+\cos\beta = 2\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}, \cos\alpha-\cos\beta = -2\sin\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2},\\ \end{align} \]万能公式如\( u= \tan \frac{x}{2} (-\pi \lt x \lt \pi) \),则\(\sin x = \frac{2u}{1+u^2},\cos x = \frac{1-u^2}{1+u^2}\)
反函数 #
设函数 \(y=f(x)\),若变量 \(y\) 在函数的值域内任取一值 \(y_0\) 时,变量 \(x\) 在函数的定义域内必有唯一值 \(x_0\) 与之对应,即 \(f(x_0) = y_0\), 那么变量 \(x\) 是变量 \(y\) 的函数。这个函数用 \(x=\phi(y)\) 来表示,称为函数 \(y=f(x)\) 的反函数
【注】
- 同一坐标平面内,函数 \(y=f(x)\) 与函数 \(x=\phi(y)\) 的图形是一样的
- 函数 \(y=f(x)\) 与函数 \(y=\phi(x)\) 的图形是关于直线y=x对称的,相当于x与y互换,x=y,定义域与值域互换
- 反函数存在定理:若 \(y=f(x)\) 在 \((a,b)\) 上严格增(减)(即 \(y\) 的值可以唯一确定 \(x\) 的值),其值域为 \(\mathbb{R}\),则它的反函数必然在 \(\mathbb{R}\) 确定,且严格增(减)
复合函数 #
设函数 \(y=f(u)\) 的定义域为 \(D_f\),而函数 \(u=\phi(x)\) 的值域为 \(R_\phi\),若 \(D_f \cap R_\phi \ne \emptyset \),则称函数 \( y=f[\phi(x)] \) 为 \(x\) 的复合函数。其中,\(x\) 称为自变量,\(y\) 称为因变量,\(u\) 称为中间变量
例如,设有函数 \(y=f(u)=\sqrt{u}, u = \phi(x) = x^2 + 1\), 其中 \(y=f(u)\) 的定义域 \([0, +\infty)\) 与 \(u = \phi(x)\) 的值域 \([1,+\infty)\) 交集非空,所以函数 \( y = f[\phi(x)] = \sqrt{x^2 + 1} \) 构成自变量 \(x\) 的复合函数
【注】
- 复合函数可由两个以上的函数经过复合构成
- 按定义,两个函数构成复合函数是有一定条件的,不是任何两个函数都可以复合成一个复合函数。例如,函数 \(y=\frac{1}{\sqrt{u}}\) 与 \(y=-x^2\) 就不能构成复合函数
特殊/分段函数 #
狄利克雷函数 #
\[ D(x) = \begin{cases} 1, & \text{if } x \text{ is rational}, \\ 0, & \text{if } x \text{ is irrational}. \end{cases} \]用于判别自变量是有理数还是无理数的函数,可作为很多事情的反例,具有以下性质:
- 定义在整个数轴上,无法画出图像
- 以任何正有理数为其周期(从而无最小正周期)
- 处处无极限、不连续、不可导
- 是偶函数
取整函数 #
一类将实数映射到相近的整数的函数,常用的取整函数有两个,分别是下取整函数(floor function)和上取整函数(ceiling function),一般涉及到的是下取整函数,在数学中一般记作[x]或者⌊x⌋,称作高斯符号,首次出现在高斯的数学著作《算术研究》,在计算机科学中一般记作floor(x),表示不超过\(x\)的整数中最大的一个
举例来说,[3.633]=3,[56]=56,[−2]=−2,[−2.263]=−3
具有以下性质:
- 按定义:\([x]\leq x<[x]+1\),当且仅当 \(x\) 为整数时取等号。
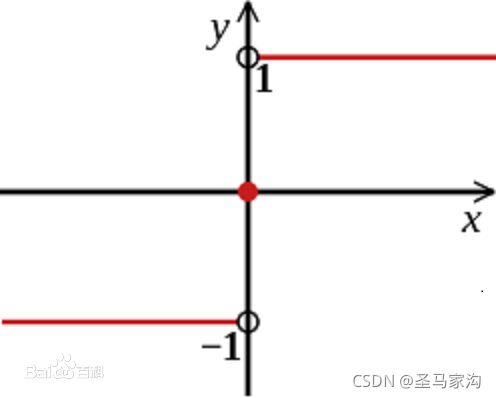
符号函数 #
\[ sgn(x) = \begin{cases} -1, & x < 0 \\ 0, & x = 0 \\ 1, & x > 0 \\ \end{cases} \]用以判断自变量的正负号,具有以下性质:
- 任何实数都可以表示为其绝对值和符号函数的积: $$ x = sgn(x)|x|,若x\neq0,sgn(x) = \frac{|x|}{x} $$
- 符号函数是绝对值函数的导数: $$ \frac{d|x|}{dx} = \frac{|x|}{x} = sgn(x) $$
- 符号函数可微分,其导数为0(除了在0)
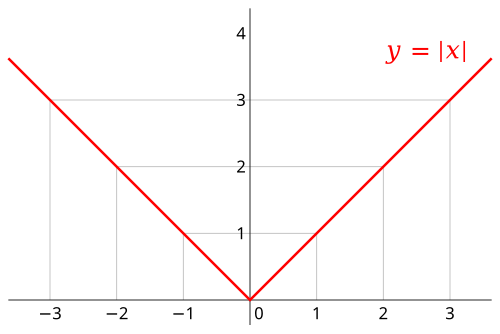
绝对值函数 #
\[ y=abs(x)=|x|= \begin{cases} x, & x \ge 0 \\ -x, & x < 0 \end{cases} \]具有以下性质:
- 是偶函数,连续函数
- 函数在原点连续,但不可导(即连续的函数不一定可导);在原点不可微,其他点处可微
- 与符号函数的关系:\(∣x∣=sgn(x)·x\) 或 \(x=sgn(x)·∣x∣\)。
最值函数 #
\[ U = \max\{f(x), g(x)\}, \quad V = \min\{f(x), g(x)\} \]具有以下性质:
\[ \begin{align} U = \frac{f(x) + g(x) + |f(x) - g(x)|}{2} \\ V = \frac{f(x) + g(x) - |f(x) - g(x)|}{2} \\ U + V = f(x) + g(x) \\ U - V = |f(x) - g(x)| \\ U * V = f(x) * g(x) \end{align} \]双曲函数 #
双曲正弦
$$ sinhx = \frac{e^x-e^{-x}}{2}\\ 定义域为(-\infty,+\infty),奇函数,在定义域内单调递增 $$双曲余弦
$$ coshx = \frac{e^x+e^{-x}}{2}\\ 定义域为(-\infty,+\infty),偶函数,在(-\infty,0)单调递减,在(0,+\infty)单调递增 $$双曲正切
$$ tanhx = \frac{sinhx}{coshx} = \frac{e^x-e^{-x}}{e^x+e^{-x}} 定义域为(-\infty,+\infty),奇函数,在定义域内单调递增 $$反双曲正弦
$$ arsinhx = \ln(x+\sqrt{x^2+1})\\ 定义域为(-\infty,+\infty),奇函数,在定义域内单调递增 $$反双曲余弦
$$ arcoshx = \ln(x+\sqrt{x^2-1})\\ 定义域为[1,+\infty),值域为[0,+\infty),在定义域内单调递增 $$反双曲正切
$$ artanhx = \frac{1}{2}\ln\frac{1+x}{1-x}\\ 定义域为(-1,+1),奇函数,在定义域内单调递增 $$