在数学上只研究与起点无关的向量,自由向量。
如果两个向量a和b的大小相等,且方向相同,我们就说向量a和b是相等的,记作\(\vec{a}=\vec{b}\)。即经过平行移动后能完全重合的向量是相等的。
共线:两个平行向量起点放在一起,它们的终点和公共起点在一条直线上
共面:\(k(k\ge3)\)个向量起点放在一起,\(k\)个终点和公共起点在一个平面上
\(xOy\)平面上的点坐标为\((x,y,0)\) x轴上的点坐标为\((x,0,0)\),其余类似
线性运算:
- 三角形法则
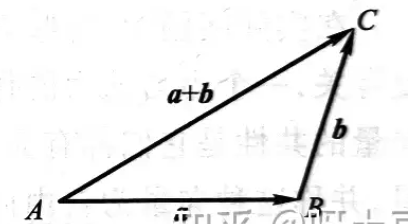
- 平行四边型法则
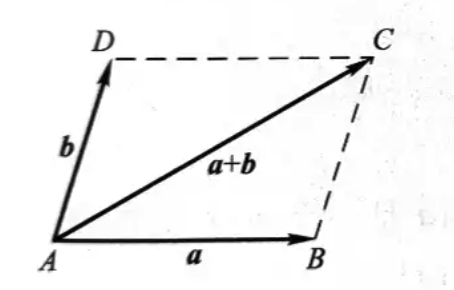
交换律:\(\vec{a} + \vec{b} = \vec{b} + \vec{a} \)
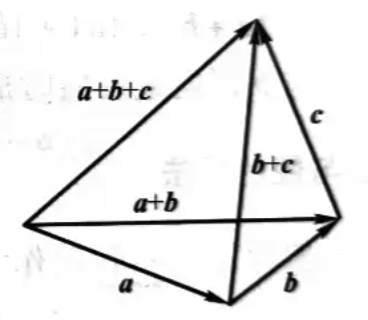
结合律:\(\vec{a} + (\vec{b} + \vec{c}) = (\vec{a} + \vec{b}) + \vec{c} \)
\(\lambda(\mu\vec{a}) = \mu(\lambda\vec{a}) = (\mu\lambda)\vec{a} \)
分配律:\((\lambda + \mu) \vec{a} = \lambda\vec{a} + \mu\vec{a}\)
单位向量:一个非零向量除以它的模的结果是一个与原向量同方向的单位向量
向量平行:设向量 \(\vec{a} \ne 0\),则向量 \(\vec{b}\) 平行于 \(\vec{a}\) 的充分必要条件是:存在唯一的实数\(\lambda,使\vec{b} = \lambda\vec{a}\)
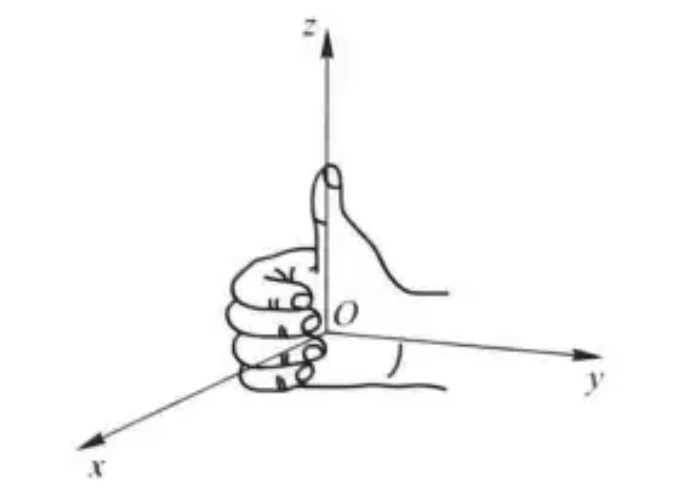
空间直角坐标系,右手准则:
向量的模、方向角、投影
向量的模:向量的大小(两点间的距离公式)叫做向量的模 零向量:模等于零,它的方向可以看做是任意的,零向量与任意向量都平行,也都垂直
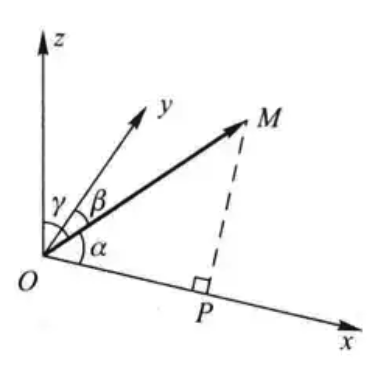
\[ \begin{align} \vec{a} = \vec{M_1M_2} & = \vec{OM_2} - \vec{OM_1} \\ & = (x_2-x_1)\vec{i} + (y_2-y_1)\vec{j} + (z_2-z_1)\vec{k} = (x_2-x_1, y_2 - y_1, z_2-z_1) \\ |\vec{a}| = \sqrt{(x_2-x_1)^2 + (y_2 - y_1)^2 + (z_2-z_1)^2} \\ \end{align} \]方向角: 非零向量 \(\vec{r}\) 与三条坐标轴的夹角 \(\alpha,\beta,\gamma\) 称为向量 \(\vec{r}\) 的方向角
\[ \begin{align} \cos\alpha = \frac{|OP|}{|OM|} = \frac{x}{|\vec{r}|} \end{align} \]类似可得 \(\cos\beta,\cos\gamma\),从而
\[ \begin{align} (\cos\alpha,\cos\beta,\cos\gamma) = (\frac{x}{|\vec{r}|},\frac{y}{|\vec{r}|},\frac{z}{|\vec{r}|}) = \frac{1}{|\vec{r}|}(x,y,z) = \frac{\vec{r}}{|\vec{r}|} = \vec{e_r} \end{align} \]\(\cos\alpha,\cos\beta,\cos\gamma\) 称为向量 \(\vec{r}\) 的方向余弦,以向量 \(\vec{r}\) 的方向余弦为坐标的向量就是与 \(\vec{r}\) 同方向的单位向量 \(\vec{e_r}\)
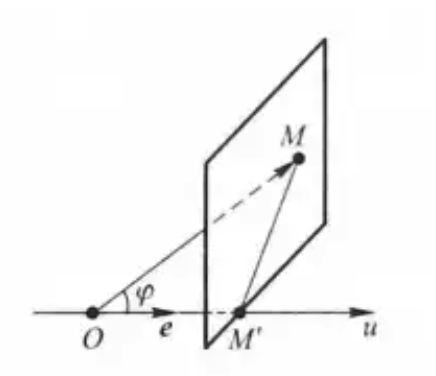
向量 \(\vec{OM'}\) 称为向量 \(\vec{OM}\) 在 \(u\) 轴上的分向量,设 \(\vec{OM'} = \lambda\vec{e}\),则数 \(\lambda\) 称为向量 \(\vec{r}\) 在 \(u\) 轴上的投影
向量 \(\vec{a}\) 在直角坐标系 \(Oxyz\) 中的坐标 \(a_x,a_y,a_z\) 就是 \(\vec{a}\) 在三条坐标轴上的投影
向量 \(\vec{a}\) 在 \(\vec{b}\) 上的投影:\( \vec{Prj}_b a = |\vec{a}|\cos < a,b> = \frac{a \cdot b}{|b|} \)
数量积
\(\vec{a}\cdot\vec{b} = |\vec{a}||\vec{b}|\cos\theta = \vec{Prj}_ba|b| \),两向量的数量积等于其中一个向量的模和另一个向量在这向量的方向上的投影的乘积
坐标表达式:两个向量的数量积等于它们对应坐标的乘积的和,若 \(a=(x_1,y_1),b=(x_2,y_2)\),则 \(a·b=x_1·x_2+y_1·y_2\)
\(\cos\theta = \frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|} = \frac{x_1·x_2+y_1·y_2}{\sqrt{x_1^2+y_1^2}\cdot\sqrt{x_2^2+y_2^2}}\)
\(\vec{a}\cdot\vec{a} = |a^2| \)
\(\vec{a}\cdot\vec{b} = 0,a \perp b = 0 \)
交换律:\(\vec{a}\cdot\vec{b} = \vec{b}\cdot\vec{a}\)
分配律:\((\vec{a}+\vec{b})\cdot\vec{c} = \vec{a}\cdot \vec{c} + \vec{a}\cdot \vec{b}\)
结合律:\((\lambda \vec{a})\vec{b} = \lambda\vec{a}\vec{b}\)
向量积
向量 \(c = a \times b\),其中\(c\)的模,\(|c| = |a||b|\sin\theta\),其中 \(\theta\) 为 \(a,b\) 之间的夹角
\(c\) 的方向垂直于 \(a与b\) 所决定的平面,\(c\) 的指向按照右手定则从 \(a\) 转向 \(b\)
\[ \begin{align} \vec{a}\times\vec{a} = \vec{0} \\ a // b 充分必要条件 \vec{a}\times\vec{b} = \vec{0} \\ \vec{a}\times\vec{b} = -\vec{b}\times\vec{a} \\ (\vec{a}+\vec{b})\times\vec{c} = \vec{a}\times\vec{c}+\vec{b}\times\vec{c} \\ (\lambda\vec{a}) \times \vec{b} = \lambda(\vec{a} \times \vec{b}) \\ \end{align} \]坐标表达式:\(\vec{a}\times\vec{b} = (a_yb_z-a_zb_y)\mathbf{i} + (a_zb_x-b_za_x)\mathbf{j} + (a_xb_y-a_yb_x)\mathbf{k} \)
\[ \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix} \]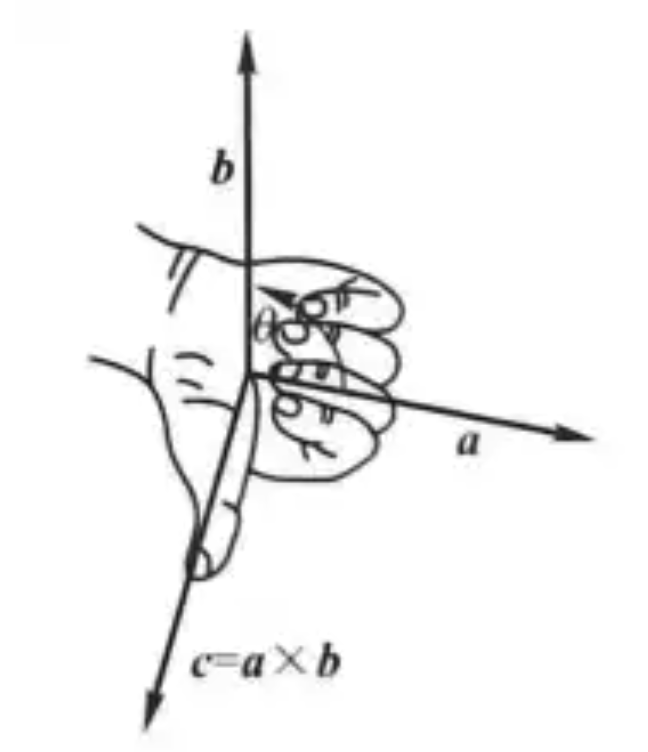
两向量位置关系
\[ \begin{align} & (1)\quad a // b \Leftrightarrow a\times b = \vec{0} \Leftrightarrow a = \lambda b \Leftrightarrow \frac{a_x}{b_x} = \frac{a_y}{b_y} = \frac{a_z}{b_z} = \lambda(\lambda为常数) \\ & (2)\quad a \perp b \Leftrightarrow a \cdot b = 0 \Leftrightarrow a_xb_x+a_yb_y+a_zb_z = 0 \end{align} \]平面向量基本定理:同一平面内的任一向量都可以表示为其他两个不共线向量的线性组合
如果 \(\vec{e_1},\vec{e_2}\) 是同一平面的两个不共线向量,那么对于这一平面内的任一向量 \(\vec{a}\),有且只有一对实数 \(\lambda_1,\lambda_2\),使 \(\vec{a}=\lambda_1\vec{e_1}+\lambda_2\vec{e_2}\)