点法式方程

法线向量：如果一个非零向量垂直于一个平面，这向量就叫该平面的法线向量

\(M_0(x_0,y_0,z_0)\) 及它的法线向量 \(n=(A,B,C)\)

\(n\cdot\vec{MM_0} = 0 即 A(x-x_0) + B(y-y_0) + C(z-z_0) = 0\) 叫做平面的点法式方程

一般方程

\(Ax + By +Cz + D = 0 \)

• 当 \(D=0\) 时，\(Ax + By +Cz = 0\) 表示一个通过原点的平面
• 当 \(A=0\) 时，\(By +Cz+D = 0\) 法线向量 \((0,B,C)\) 垂直于 \(x\) 轴，方程表示平行于 \(x\) 轴的平面
• 当 \(A=B=0\) 时，\(Cz+D = 0\) 法线向量 \((0,0,C)\) 同时垂直于 \(x\) 轴和\(y\) 轴，方程表示平行于 \(xOy\) 面的平面

截距式方程

\(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\)

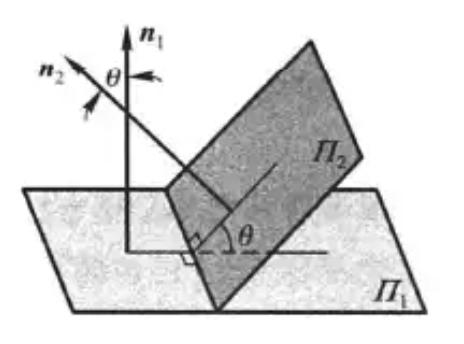
两平面夹角

两平面的法线向量的夹角(通常指锐角或直角)称为两平面的夹角。 \ \(\cos\theta = |\cos< n_1,n_2>| = \frac{|A_1A_2+B_1B_2+C_1C_2|}{\sqrt{A_1^2+B_1^2+C_1^2}\cdot\sqrt{A_2^2+B_2^2+C_2^2}} \)

互相垂直：\(A_1A_2+B_1B_2+C_1C_2 = 0\)

平行或重合：\(\frac{A_1}{A_2} = \frac{B_1}{B_2} = \frac{C_1}{C_2}\) (重合=\(\frac{D_1}{D_2}\))

点到面的距离公式

\(d = \frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}}\)

两平面之间的距离公式
\(d = \frac{|D_1 - D_2|}{\sqrt{A^2+B^2+C^2}}\)