球面

球面方程：\((x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2 = R^2 \)
一般式：\(x^2+y^2+z^2+Dx+Ey+Fz+G = 0 \)
球心：\((-\frac{D}{2},-\frac{E}{2},-\frac{F}{2}) \)
半径R：\(\frac{\sqrt{D^2+E^2+F^2-4G}}{2}\)

旋转曲面：以一条平面曲线绕其平面上的一条直线旋转一周所成的曲面

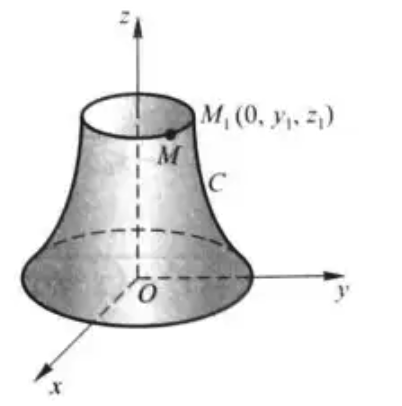
设在 \(yOz\) 坐标面上有一已知曲线 \(C\)，它的方程为：\(f(y,z) = 0\) 把这曲线绕 \(z\) 轴旋转一周，得到一个以 \(z\) 轴为轴的旋转曲面 \(f(\pm\sqrt{x^2+y^2},z) = 0\)

圆柱面：\(x^2 + y^2 = R^2 \) 缺什么，沿什么轴为准线移动

二次曲面：由二次多项式方程定义的曲面

椭圆锥面：
\(\frac{x^2}{a^2} + \frac{y^2}{b^2} = z^2 \) 以垂直于 \(z\) 轴的平面 \(z=t\) 截此曲面，当 \(t=0\) 时得一点 \((0,0,0)\)；当 \(t \ne 0\) 时，得平面 \(z=t\) 上的椭圆为 \(\frac{x^2}{(at)^2} + \frac{y^2}{(bt)^2} = 1 \)

椭球面：\(\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1 \)

其他 TODO

空间曲线及其方程

一般方程

消去变量\(z\)可得 \(H(x,y)=0\)，表示母线平行 \(z\) 轴的柱面，显然该曲线上的点必定在此柱面上，\ 此柱面称为空间曲线关于 \(xOy\) 坐标面的投影柱面；其他轴同理