邻域
在二维平面内的 \( \delta \) 邻域是关于一个点 \(P_0(x_0, y_0)\) 的。所有和该点的距离小于某正数 \( \delta \) 的点的全体,称为点 \(P_0(x_0, y_0)\) 的\( \delta \) 领域,记为 \(U(P_0,\delta)\)。
\[ U(P_0,\delta) = \{P| |PP_0| < \delta \} \]或
\[ U(P_0,\delta) = \{(x,y) | \sqrt{(x-x_0)^2 + (y-y_0)^2} < \delta \} \]去心邻域
不包含 \(P_0\)点的邻域。
\(\mathring{U}(P_0, \delta) = \{ P \mid 0 < |PP_0| < \delta \}\)。如果不需要强调邻域的半径 \(\delta\),则其去心邻域记作 \(\mathring{U}(P_0)\)。
极限
若函数 \(f(x,y)\) 在区域 \(D\) 上有定义, \(P_0\) 在区域内或边界上,对于\( \forall \varepsilon > 0\),总 \(\exists \delta > 0\),且满足 \(0 < |PP_0| < \delta\),恒有:
\[ |f(x,y) -A| < \varepsilon \],则称常数A为\(x,y) \to (x_0,y_0)\) 时 \(f(x,y)\) 的极限,记作:
\[ \lim_{(x,y) \to (x_0,y_0)}f(x,y) = A \]这种极限我们一般称之为:二重极限。
连续
如果 \(\lim_{(x,y) \to (x_0,y_0)}f(x,y) = f(x_0,y_0)\),则称函数在 \((x_0,y_0)\)点连续。
如果函数在区域上每个点都连续,则函数在区域上连续。
偏导数
函数 \(z = f(x,y) \)在点\((x_0,y_0)\)某领域有定义,如果极限:
\[ \lim_{\Delta x \to 0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x} \]存在,则此极限为函数在 \((x_0,y_0)\)处对 \(x\) 的偏导数,记作:
\[ \frac{\partial z}{\partial x} \Big|_{x=x_0, y=y_0}, \quad \frac{\partial f}{\partial x} \Big|_{x=x_0, y=y_0}, \quad z'_x \Big|_{x=x_0, y=y_0} \quad \text{或}, \quad f'_x(x_0, y_0) \]对 \(y\) 求偏导数同理,此处不再赘述。
偏导函数
若函数 \(z = f(x,y) \) 在区域 \(D\) 上的每一点都有偏导数,则偏导数的集合(一般来说也是 \((x,y)\) 的函数)称为\(f(x,y)\)的偏导函数,简称偏导数,记作:
\[ \frac{\partial z}{\partial x}, \quad \frac{\partial f}{\partial x}, \quad f'_x(x, y) \]高阶偏导数
若函数 \(z = f(x,y) \) 的偏导数仍有偏导数,则称之为二阶偏导数。
\[ \begin{align} \frac{\partial^2 z}{\partial x^2} = \frac{\partial}{\partial x} \left( \frac{\partial z}{\partial x} \right) = f''_{xx}(x, y) = z''_{xx} \\ \frac{\partial^2 z}{\partial x \partial y} = \frac{\partial}{\partial y} \left( \frac{\partial z}{\partial x} \right) = f''_{xy}(x, y) = z''_{xy} \end{align} \]其中\(f_{xy}'', f_{yx}''\)称为二阶混合偏导数。类似的可以定义 \(n(n \ge 3)\) 阶偏导数。
如果 函数 \(z = f(x,y) \) 的两个二阶混合偏导数 \(f_{xy}'', f_{yx}''\)都在区域连续,则区域内:
\(f_{xy}'' = f_{yx}''\)
二阶混合偏导数在连续的条件下与求导的顺序无关。
可微
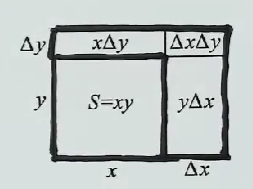
长方形 \(x,y\) 面积的增量为:
\[ \Delta S = (x+\Delta x)(y+\Delta y) - xy = y\Delta x + x\Delta y + \Delta x \Delta y \]- \(y\Delta x + x\Delta y\): 关于 \(\Delta x, \Delta y\) 的线性函数
- \(\Delta x \Delta y\): 关于 \(\rho = \sqrt{(\Delta x)^2 + (\Delta y)^2} \) 的高阶无穷小量。即: \[ \Delta S = y\Delta x + x\Delta y + o(\rho )(\rho \to 0) \]
\(y\Delta x + x\Delta y\) 是 \(\Delta S\)的主要部分,\(o(\rho )\) 是 \(\Delta S\) 与 \(y\Delta x + x\Delta y\) 之间的误差,称 \(y\Delta x + x\Delta y\) 为函数 \(S = xy\) 在点 \((x,y)\) 处的全微分。
设函数 \(z=f(x,y)\) 在点 \((x,y)\) 的某实心领域内有定义,若该点的全增量
\[ \Delta z = f(x+\Delta x, y+\Delta y) - f(x,y) \]可表示为
\[ \Delta z = A\Delta x + B\Delta y + o(\rho ) \]其中A,B