概念 #

微分方程(Differential Equation)是包含未知函数及其导数的方程。未知函数导数的最高阶数称为该微分方程的阶。

若未知函数是一元函数的微分方程称为常微分方程(Ordinary Differential Equation, ODE) ：

如果微分方程是关于未知函数及各阶导数的线性表达式（将只包含 \(x\) 的项视为常数），则称为 n 阶线性(linear)常微分方程。

若未知函数是多元函数，方程中含有自变量的偏微分，称之为偏微分方程(Partial Differential Equations, PDE)。

如

如果将一个函数 \(y = \varphi(x)\) 其各阶导数代入微分方程得到恒等式：

则称 \(y = \varphi(x)\) 为上述方程的一个解(solution)。n 阶微分方程的解 \(y = \varphi\left(x, C_1, C_2, \cdots, C_n\right)\) 含有 n 个相互独立的任意常数 \(C_1, C_2, \cdots, C_n\)，则称为该微分方程的通解(general solution)，称不包含任意常数的解为特解(particular solution)。

通常为了解决实际问题，确定常数的值，需要引入初值条件(initial conditions)。初值条件联合微分方程组成初值问题(Initial Value Problem, IVP)。一阶常微分方程的初值问题通常记作：

例子 #

已知一静止物体质量为 \(1kg\)，受到向右的力 \(F\)，大小为\(|F| = 2t\) ，求速率 \(v\) 与时间 \(t\) 的关系。

解：根据牛顿第二定律，\(F = ma \Rightarrow F = m\frac{dv}{dt} = 2t\)，代入 \(m = 1\)，得

\(\frac{dv}{dt} = 2t\)，整理可得 \(dv = 2tdt\)，两边积分：

\(\int{dv} = \int{2tdt}\)，得 \(v=t^2+c\)，根据\(t=0\)时，\(v=0\)，可得 \(C=0\)，从而得到

\(v=t^2\)

衰减模型，应用场景碳-14测年（Carbon-14 dating）等

\( x' = -rx \)，其中 \(r\) 为衰减率，这里假定为固定值，\(x\) 为关于 \(t\) 的函数

可以表示为 \(\frac{x'}{x} = -r \)，

观察发现\(\frac{x'}{x} = \frac{d}{dt} \ln x\)，可得 \( \frac{d}{dt} \ln x\ = -r \)，两边对 \(t\) 积分

\( \int{\frac{d}{dt} \ln x} dt = - \int r dt \)，可得

\(\ln x = -rt + C_1\)，其中 \(C_1\) 为任意常数，进一步化简

\( x = e^{-rt + C_1} = e^{C_1}e^{-rt} = Ce^{-rt}\)，其中 \(C = e^{C_1}\) 也为任意常数

如果对 \(x(t)\) 施加初始条件如\(x(0) = x0\)，则能确定任意常数C

解的几何意义 #

微分方程的解对应的曲线称为积分曲线(integral curve或solution curve)。若不给定初始条件，微分方程的通解在几何上对应着一族积分曲线，称为积分曲线族(family of integral curves)。

考虑微分方程 \(y'=f(x,y)\)，此方程的解有如下几何意义：
积分曲线在\(xy\) 平面中过点 \((x,y)\)的斜率值为 \(f(x,y)\)。

若 \(f(x,y)\) 的定义域为 \(xy\) 平面 \(G\) ，在 \(G\) 内每一点 \((x,y)\) 作斜率为 \(f(x,y)\) 的单位线段，则称该线段为点 \((x,y)\) 的线素。\(G\) 内所有的线素构成由微分方程确定的线素场(line element field)或方向场(direction field)。线素场的等斜线(isocline)为拥有相同的斜率 \(f(x,y) = k\) 的所有线素。线素场的零斜线(nullclines)为斜率为零的所有线素。

所以说，方向场描绘出了微分方程积分曲线的大致走向。通过等斜线或零斜线将平面分成若干区域，分析每个区域内斜率变化规律，可以帮助推测积分曲线的大致走势。

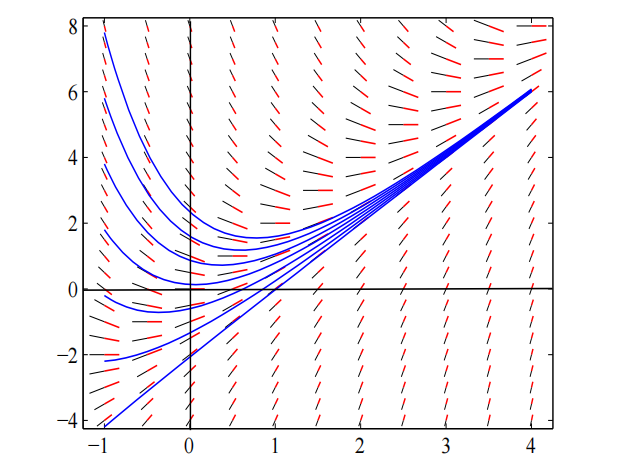
下图为微分方程 \( x' = -x + 2t, -1 \le t \le 4, -4 \le x \le 8 \) 的方向场，显示了几条解曲线；如果施加初始条件 \( x(t_0) = x_0 \) ，则对应经过点\((t_0, x_0)\)的那条。