介绍 #
Wiener攻击是一种针对使用较小的私钥解密指数进行RSA加密的攻击方法。Wiener’s theorem 的描述如下:
N = pq, q < p < 2q (即 p + q - 1 < 3sqrt(N)), d < 1/3N^(1/4)
给定的 <N,e> 满足 ed ≡ 1 (mod φ(N)),则能够有效地求得 d 的值
理解该定理需要先了解连分数和渐进分数概念
连分数(continued fraction)表现形式如下
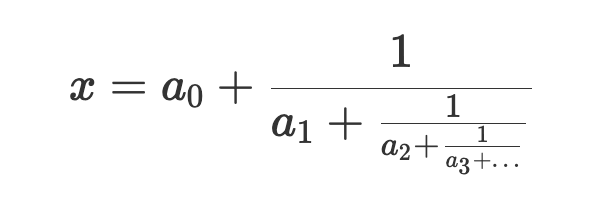
连分数可以用以下形式进行简写,叫做连分数展开(continued fraction expansion):
x = [a0,a1,a2,a3,a4,a5,...,an]
如 π =[3,7,15,1,292,1,1,1,2,…]
有理数(无理数)具有有限(无限)连分数展开式。
基于连分数可以得到渐进分数,渐进分数是有理数,可以看作是一种近似逼近。如下
c0 = 3/1 = 3.0
c1 = 3 + 1/7 = 22/7 = 3.142857
c2 = 3 + 1/(7+1/15) = 333/106 = 3.141509
c3 = 3 + 1/(7+1/(15+1/1)) = 355/113 = 3.141593
这些 ci 有理数被称为连分数的渐进分数(the convergents of a continued fraction)。ci 越来越接近 π (3.141592…)。
# Continued Fraction Expansion of Rationals
# Rationals can be reprensented by n = Nominators / d = Denominators
import math
def cf_expansion(n, d):
e = []
q = n // d
r = n % d
e.append(int(q))
while r != 0:
n, d = d, r
q = n // d
r = n % d
e.append(int(q))
return e
# math.pi: 3.141592653589793
# [3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 3, 3, 2, 1, 3, 3, 7, 2, 1, 1, 3, 2, 42, 2]
print(cf_expansion(math.pi, 1))
# 17993/90581
# [0, 5, 29, 4, 1, 3, 2, 4, 3]
print(cf_expansion(17993, 90581))
def convergents(e):
n = [] # Nominators
d = [] # Denominators
for i in range(len(e)):
if i == 0:
ni = e[i]
di = 1
elif i == 1:
ni = e[i]*e[i-1] + 1
di = e[i]
else: # i > 1
ni = e[i]*n[i-1] + n[i-2]
di = e[i]*d[i-1] + d[i-2]
n.append(ni)
d.append(di)
yield (ni, di)
e = [0, 5, 29, 4, 1, 3, 2, 4, 3]
# 0/1
# 1/5
# 29/146
# 117/589
# 146/735
# 555/2794
# 1256/6323
# 5579/28086
# 17993/90581
for n, d in convergents(e):
print("%d/%d" % (n,d))
理解上述连分数和渐进分数后,我们尝试理解 Wiener’s theorem 证明的思路
- 结合RSA实现及Wiener’s theorem中的各种限制条件,我们可以最终得到
abs(e/N - k/d) < 1/(2d^2)(详细过程请参看wiki中的证明部分)
- 根据
Legendre定理,如果abs(x - a/b) < 1/(2b^2),那么 a/b 是 x 渐进分数中的一个。体现在这里就是k/d是e/N渐进分数中的一个 - 联立以下2个式子,可以筛选出正确的
k/d值ed - kφ(N) = 1- 由
φ(N)可以推出N=pq的分解:φ(N) = N - p - q + 1 = N - p - N/p + 1->p^2 + p(φ(N) - N - 1) + N = 0,如果根 p1p2 = N,则得到正确的k/d值
- 总体上,获得了
k/d值 能推出φ(N),推出φ(N)能得到N = pq
Wiener 攻击的列子和代码实现如下:
<N,e> = <90581,17993> 求 d
e/N 的连分数扩展是 [0, 5, 29, 4, 1, 3, 2, 4, 3]
对应的 convergents 是,其中会有 k/d
0
1/5
29/146
117/589
146/735
555/2794
1256/6323
5579/28086
17993/90581
挨个判断,最终确定 1/5 为正确的 k/d,判断过程如下:
φ(N) = ed - 1 / k = 17993 * 5 - 1 / 1 = 89964
根据 p^2 + p(φ(N) - N - 1) - N = 0 即
p^2 - 618p + 90581 = 0 得 p1 = 379, p2 = 239,满足 N = 90581 = p1 x p2
import gmpy2
def cf_expansion(n, d):
e = []
q = n // d
r = n % d
e.append(int(q))
while r != 0:
n, d = d, r
q = n // d
r = n % d
e.append(int(q))
return e
def convergents(e):
n = [] # Nominators
d = [] # Denominators
for i in range(len(e)):
if i == 0:
ni = e[i]
di = 1
elif i == 1:
ni = e[i]*e[i-1] + 1
di = e[i]
else: # i > 1
ni = e[i]*n[i-1] + n[i-2]
di = e[i]*d[i-1] + d[i-2]
n.append(ni)
d.append(di)
yield ni, di
def wiener_attack(e, n):
cf = cf_expansion(e, n)
for k, d in convergents(cf):
if k == 0:
continue
phi = (e * d - 1) // k
b = phi - n - 1
delta = b * b - 4 * n
if delta < 0:
continue
root, exact = gmpy2.iroot(delta, 2)
if exact:
p, q = (-b + root) // 2, (-b - root) // 2
if p * q == n:
return p, q
# or
# p = Symbol('p', integer=True)
# roots = sympy.solve(p**2 + (phi - N - 1)*p + N, p)
# p, q = roots
# if p * q == n:
# return p, q
e = 17993
n = 90581
p, q = wiener_attack(e, n)
# p = 379
# q = 239
print("p = %d" % int(p))
print("q = %d" % int(q))
参考链接:
https://zhuanlan.zhihu.com/p/400818185
https://sagi.io/crypto-classics-wieners-rsa-attack/
https://en.wikipedia.org/wiki/Wiener%27s_attack
https://crypto.stackexchange.com/questions/56204/rsa-attack-with-continued-fractions-wieners-attack
题目 #
n = 460657813884289609896372056585544172485318117026246263899744329237492701820627219556007788200590119136173895989001382151536006853823326382892363143604314518686388786002989248800814861248595075326277099645338694977097459168530898776007293695728101976069423971696524237755227187061418202849911479124793990722597
e = 354611102441307572056572181827925899198345350228753730931089393275463916544456626894245415096107834465778409532373187125318554614722599301791528916212839368121066035541008808261534500586023652767712271625785204280964688004680328300124849680477105302519377370092578107827116821391826210972320377614967547827619
c = 430518885052463211928880150309746899793280569494514717229804457610645654546618397141033560961143804493709939917151868116850149667503379601542677290248006042112387562073597991532984562273435948997353239670931506060376329812189999562605693486930504349878154273868213374018040795628048038832072369044250913887074
思路 #
- e 比较大,推测d比较小,尝试使用 Wiener 攻击
答案
import gmpy2
import libnum
def cf_expansion(n, d):
e = []
q = n // d
r = n % d
e.append(int(q))
while r != 0:
n, d = d, r
q = n // d
r = n % d
e.append(int(q))
return e
def convergents(e):
n = [] # Nominators
d = [] # Denominators
for i in range(len(e)):
if i == 0:
ni = e[i]
di = 1
elif i == 1:
ni = e[i]*e[i-1] + 1
di = e[i]
else: # i > 1
ni = e[i]*n[i-1] + n[i-2]
di = e[i]*d[i-1] + d[i-2]
n.append(ni)
d.append(di)
yield ni, di
def wiener_attack(e, n):
cf = cf_expansion(e, n)
for k, d in convergents(cf):
if k == 0:
continue
phi = (e * d - 1) // k
b = phi - n - 1
delta = b * b - 4 * n
if delta < 0:
continue
root, exact = gmpy2.iroot(delta, 2)
if exact:
p, q = (-b + root) // 2, (-b - root) // 2
if p * q == n:
return p, q
e = 354611102441307572056572181827925899198345350228753730931089393275463916544456626894245415096107834465778409532373187125318554614722599301791528916212839368121066035541008808261534500586023652767712271625785204280964688004680328300124849680477105302519377370092578107827116821391826210972320377614967547827619
n = 460657813884289609896372056585544172485318117026246263899744329237492701820627219556007788200590119136173895989001382151536006853823326382892363143604314518686388786002989248800814861248595075326277099645338694977097459168530898776007293695728101976069423971696524237755227187061418202849911479124793990722597
p, q = wiener_attack(e, n)
# p = 28805791771260259486856902729020438686670354441296247148207862836064657849735343618207098163901787287368569768472521344635567334299356760080507454640207003
print("p = %d" % int(p))
# q = 15991846970993213322072626901560749932686325766403404864023341810735319249066370916090640926219079368845510444031400322229147771682961132420481897362843199
print("q = %d" % int(q))
c = 430518885052463211928880150309746899793280569494514717229804457610645654546618397141033560961143804493709939917151868116850149667503379601542677290248006042112387562073597991532984562273435948997353239670931506060376329812189999562605693486930504349878154273868213374018040795628048038832072369044250913887074
n = p*q
phi_n = (p-1)*(q-1)
d = libnum.invmod(e, phi_n)
m = pow(c,d,n)
print(libnum.n2s(m))
# flag{wieneR_is_n0t_diFFicuLt}